NJU-CourseNote: Principles and Techniques of Compilers - Ch09 Machine-Free Optimization.
Tips:
强烈建议修习李樾和谭添老师开设的《静态分析》课程. 该部分的理论知识更贴近于静态分析的内容, 因此本笔记会略去相关内容.
引言
- 代码优化或者代码改进
- 在目标代码中消除不必要的指令
- 把一个指令序列替换为一个完成相同功能的更快的指令序列
- 全局优化
- 具体的优化实现基于数据流分析技术
- 用以收集程序相关信息的算法
优化的主要来源
- 编译器只能通过一些相对低层的语义等价转换来优化代码
- 冗余运算的原因
- 源程序中的冗余
- 高级程序设计语言编程的副产品,如
A[i][j].f = 0; A[i][j].k = 1;
- 语义不变的优化
- 公共子表达式消除
- 复制传播
- 死代码消除
- 常量折叠
- 冗余运算的原因
基本优化技术
控制流图
- 控制流图(Control Flow Graph)
- 表示程序控制流的有向图(简称流图)
- 流图的结点是基本块
- 流图的边指明了哪些基本块可以跟在一个基本块之后运行
- 若基本块
Bi最后一条指令执行后紧跟着执行的指令可能为基本块Bj,则图上有一条边Bi -> Bj
- 若基本块
- 图上的路径表示程序执行的路径,可作为优化与分析的基础
- 它给出了程序的控制流
- 可以根据流图了解到一个值是否会被使用等信息
Exmaple:
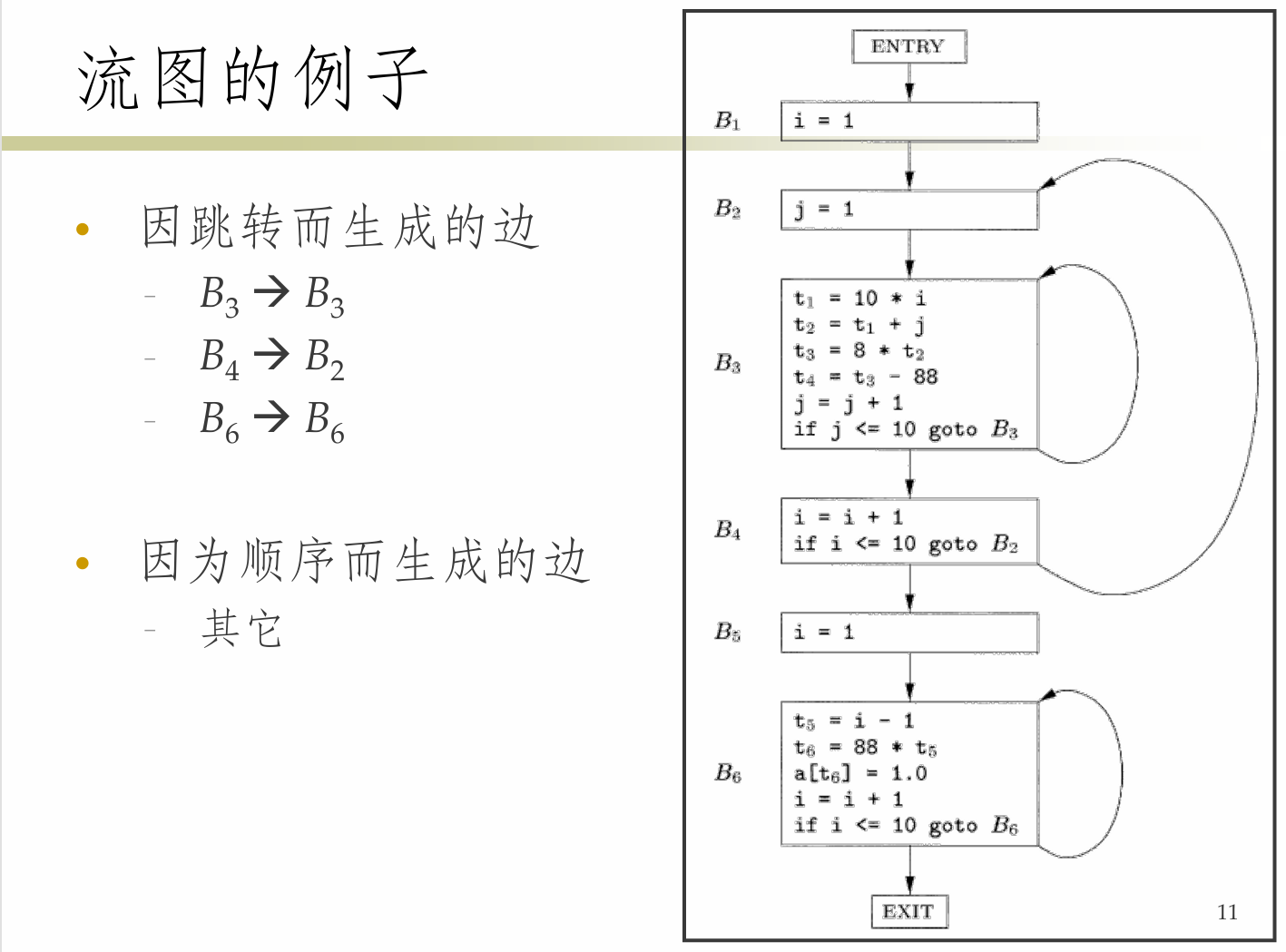
全局公共子表达式
- 公共子表达式(Common Subexpression)
- 在某次出现之前必然已被计算过
- E的运算分量在该次计算之后没有被改变
- 如果上次公共子表达式E值赋给了x,且x值没有被修改过,那么我们可使用x,而无需计算E
Example
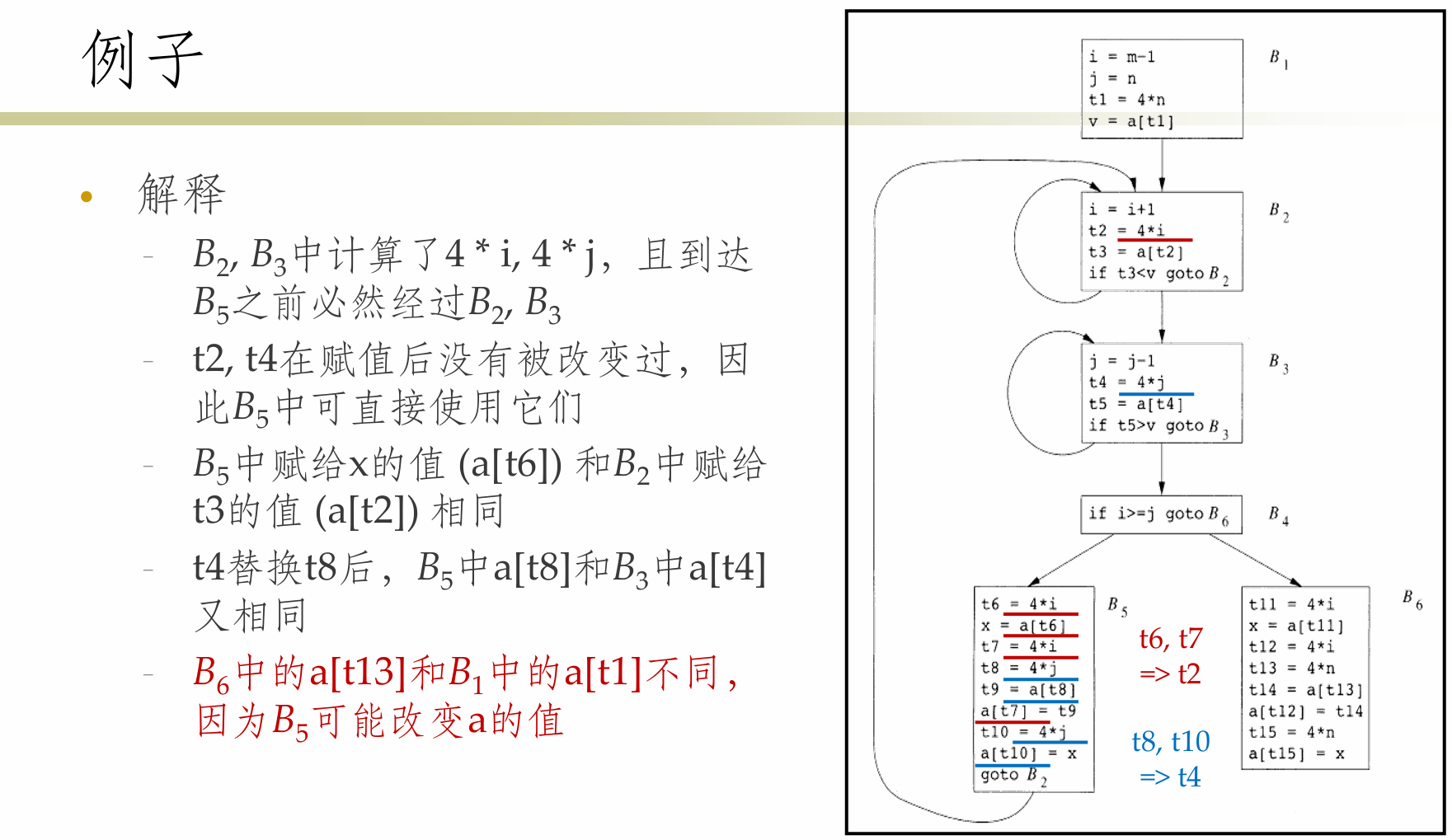
复制传播

Example
2
a[t4] = x可以被优化为
2
a[t4] = t3
死代码消除
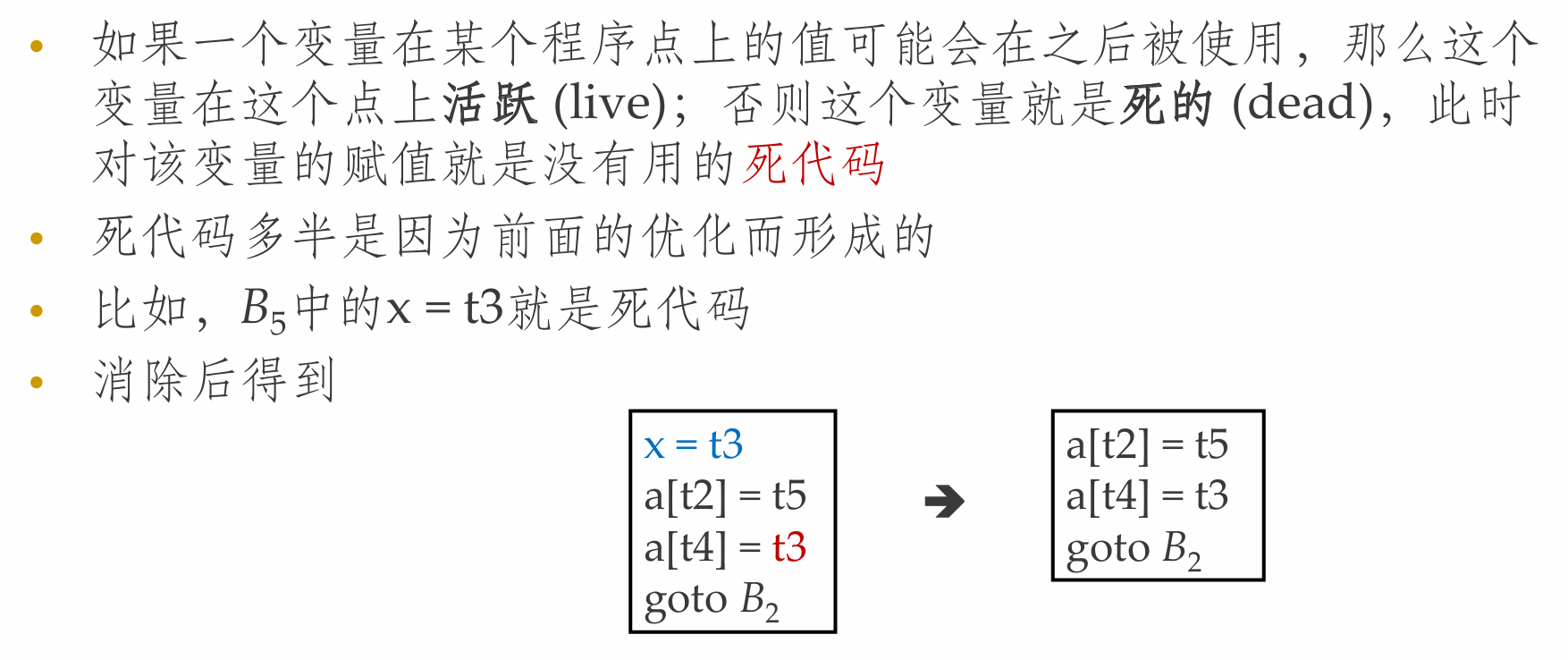
代码移动
- 循环中的代码会被执行很多次
- 循环不变表达式: 循环的同一次运行的不同迭代中,表达式的值不变
- 把循环不变表达式移动到循环入口之前计算可以提高效率
- 循环入口: 进入循环的跳转都以这个入口为目标
Example:
while (i <= limit – 2){...}如果
limit在循环体内不会改变, 则可在循环外计算limit - 2可以优化为
t = limit - 2; while(i <= t){...}
归纳变量和强度消减
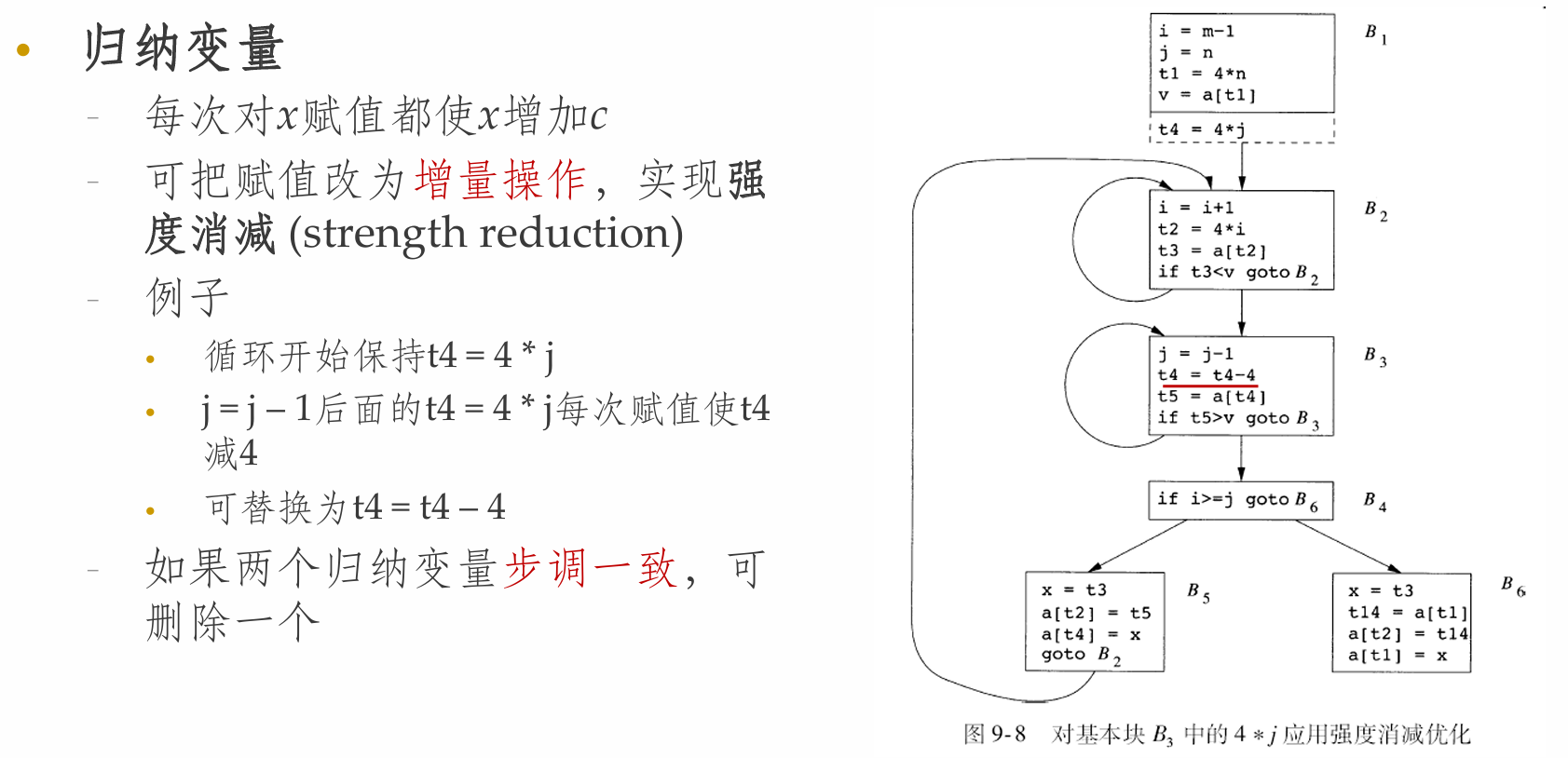
数据流分析
本处略, 参见静态分析中的数据流分析
https://cs.nju.edu.cn/tiantan/software-analysis/DFA-AP.pdf
https://cs.nju.edu.cn/tiantan/software-analysis/DFA-FD.pdf
部分冗余消除
懒惰代码移动
- 目标
- 所有不复制代码就可消除的冗余计算都被消除
- 优化后的代码不会执行原程序中不执行的任何计算
- 表达式的计算应该尽量靠后,以利于寄存器的分配
- 冗余消除
- 完全冗余
- 部分冗余:在流图中放置表达式
x + y的拷贝,使得某处的x + y成为完全冗余,从而删除
- 基本步骤
- 找出各程序点上预期执行的所有表达式
- 在表达式被预期执行但是不可用的程序点上,放置表达式的计算
- 把表达式尽量后延到某个程序点,在到达这个点的所有路径上,这个表达式在这个程序点之前被预期执行,但是还没有使用这个值
- 消除只使用一次的临时变量
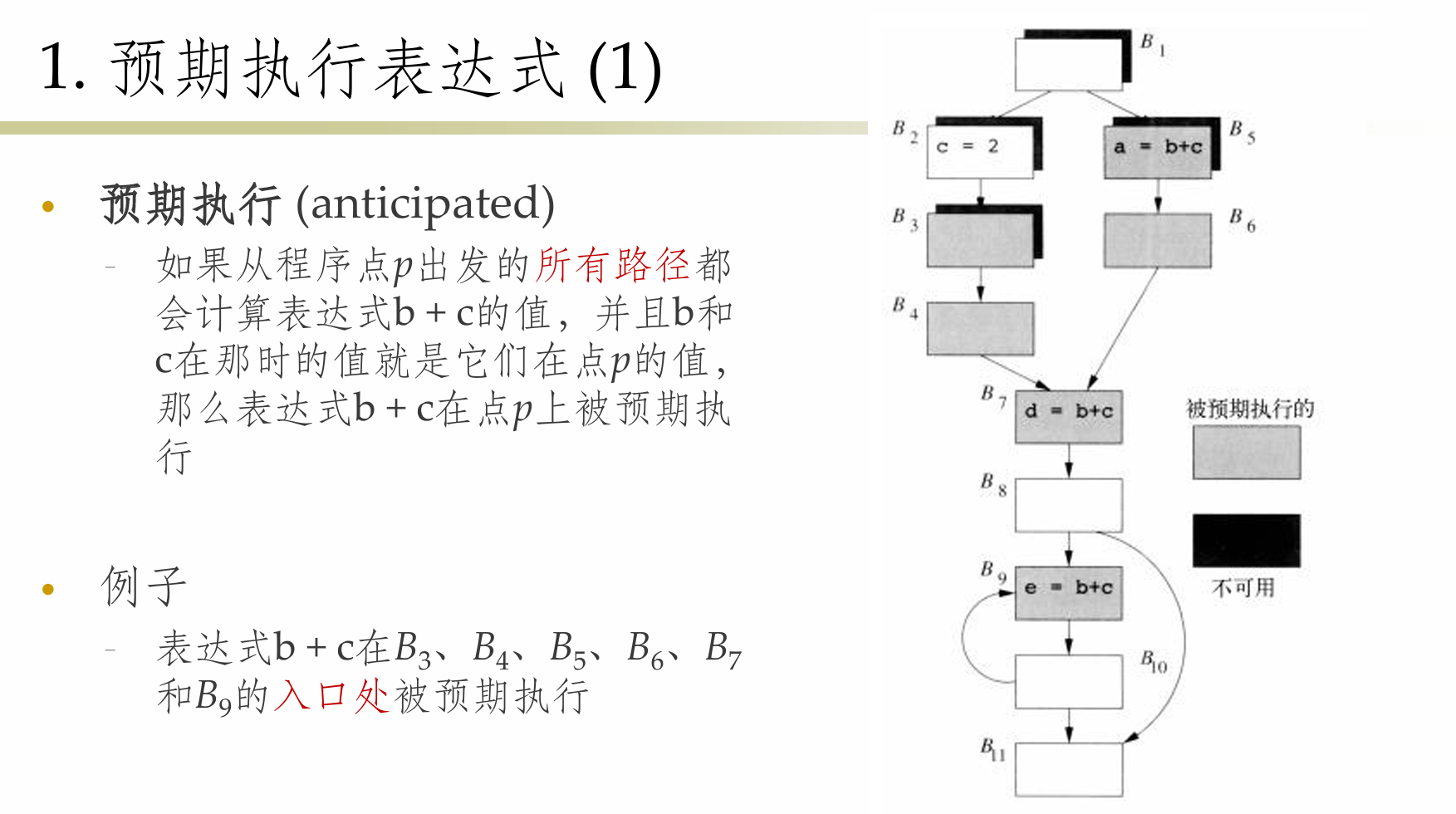
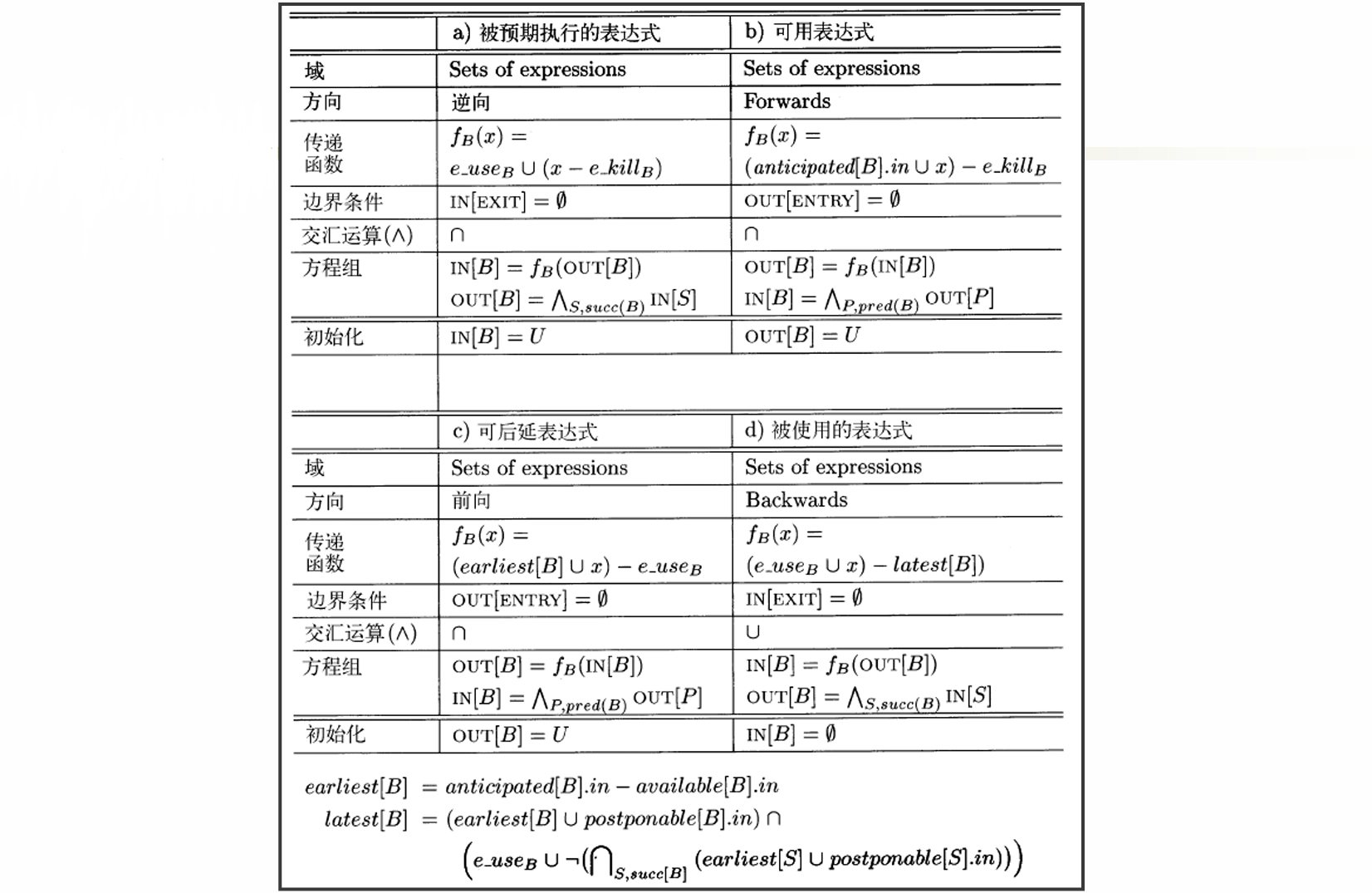
预期执行表达式

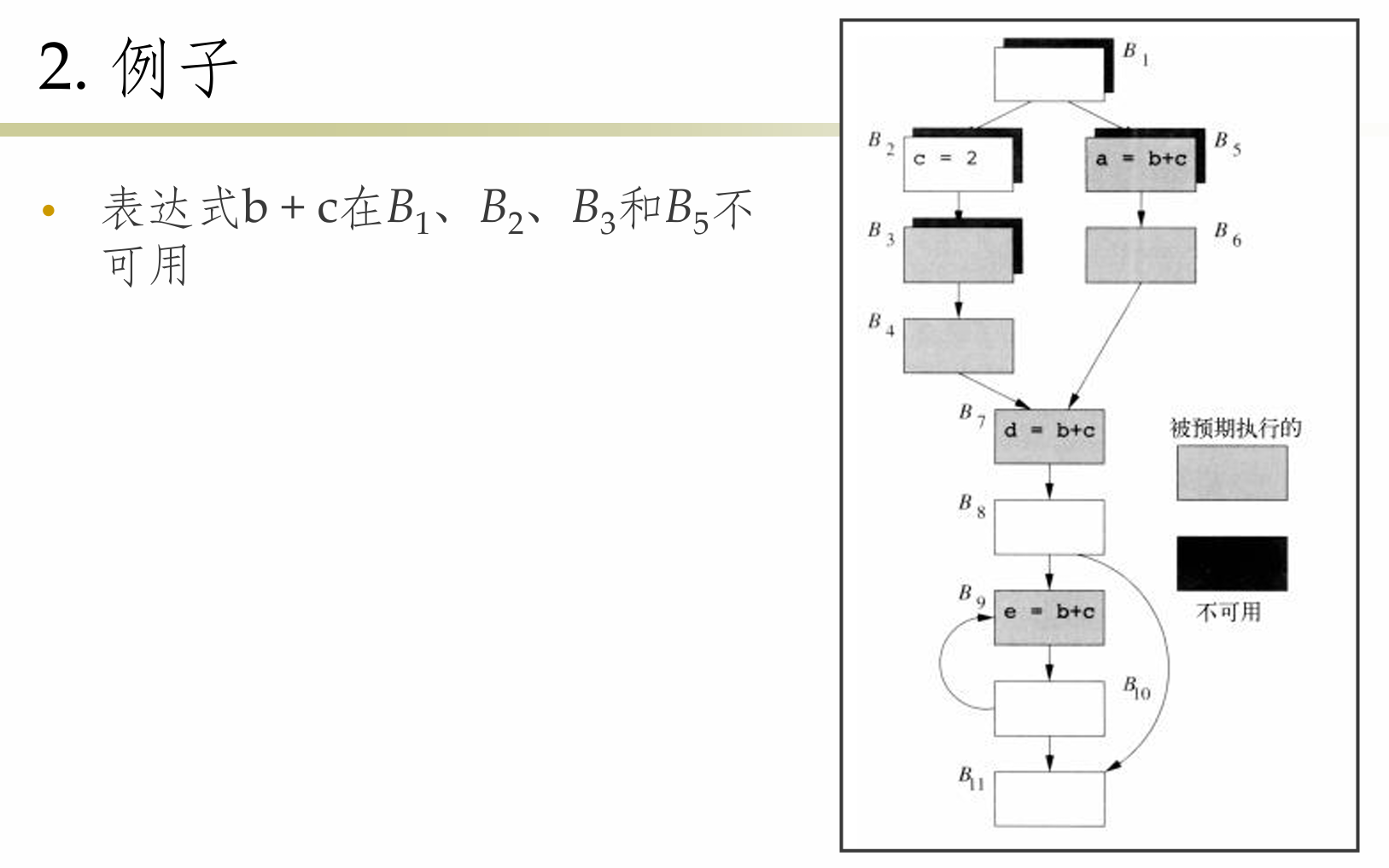
可用表达式
- 和前面的可用表达式类似,但假设代码已经被复制到了预期执行点上
- 表达式在基本块的出口处可用(available)的条件
- 在基本块的入口处可用,或在基本块的入口处的预期执行表达式中
- 且没有被这个基本块杀死
Exmaple:
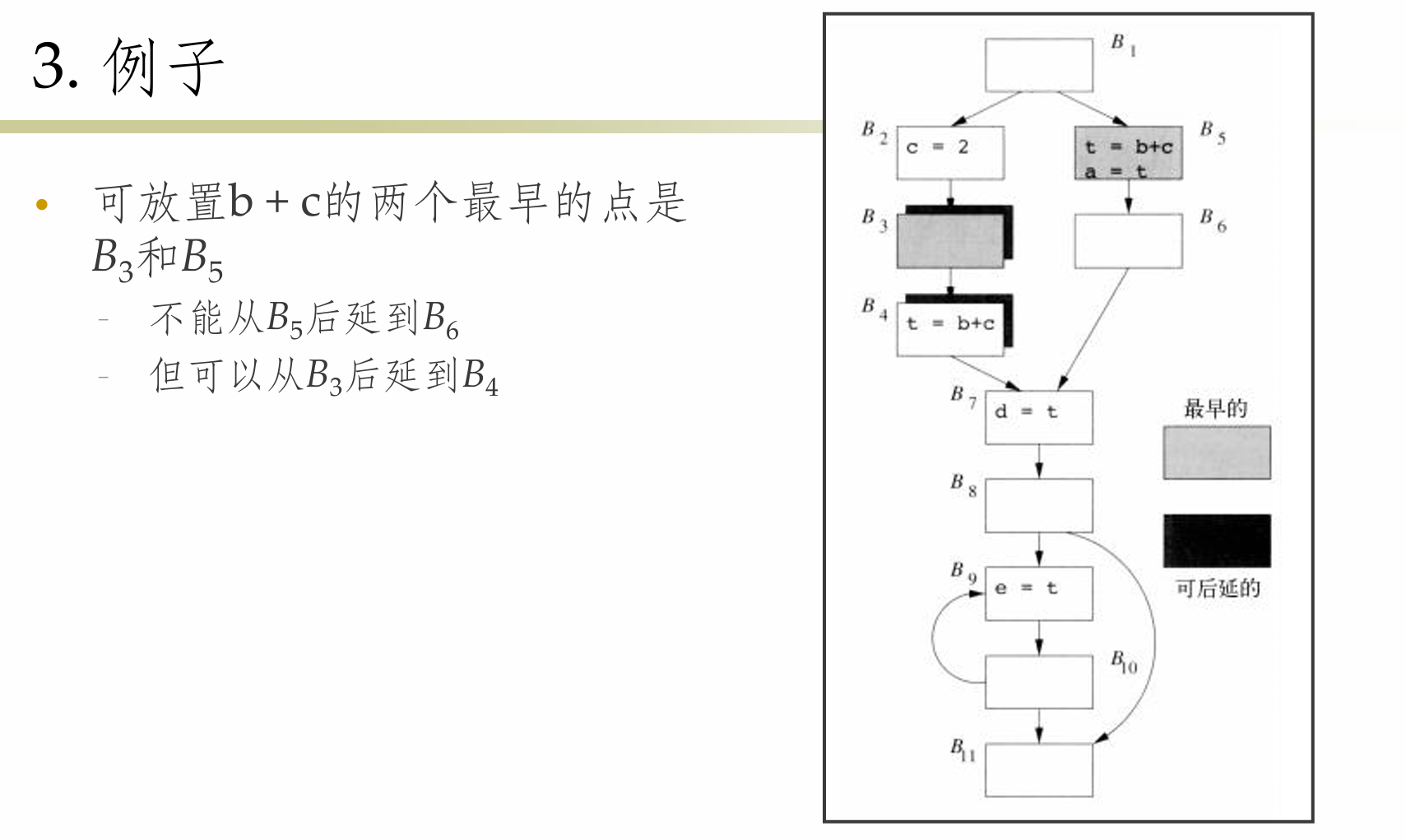
可后延表达式
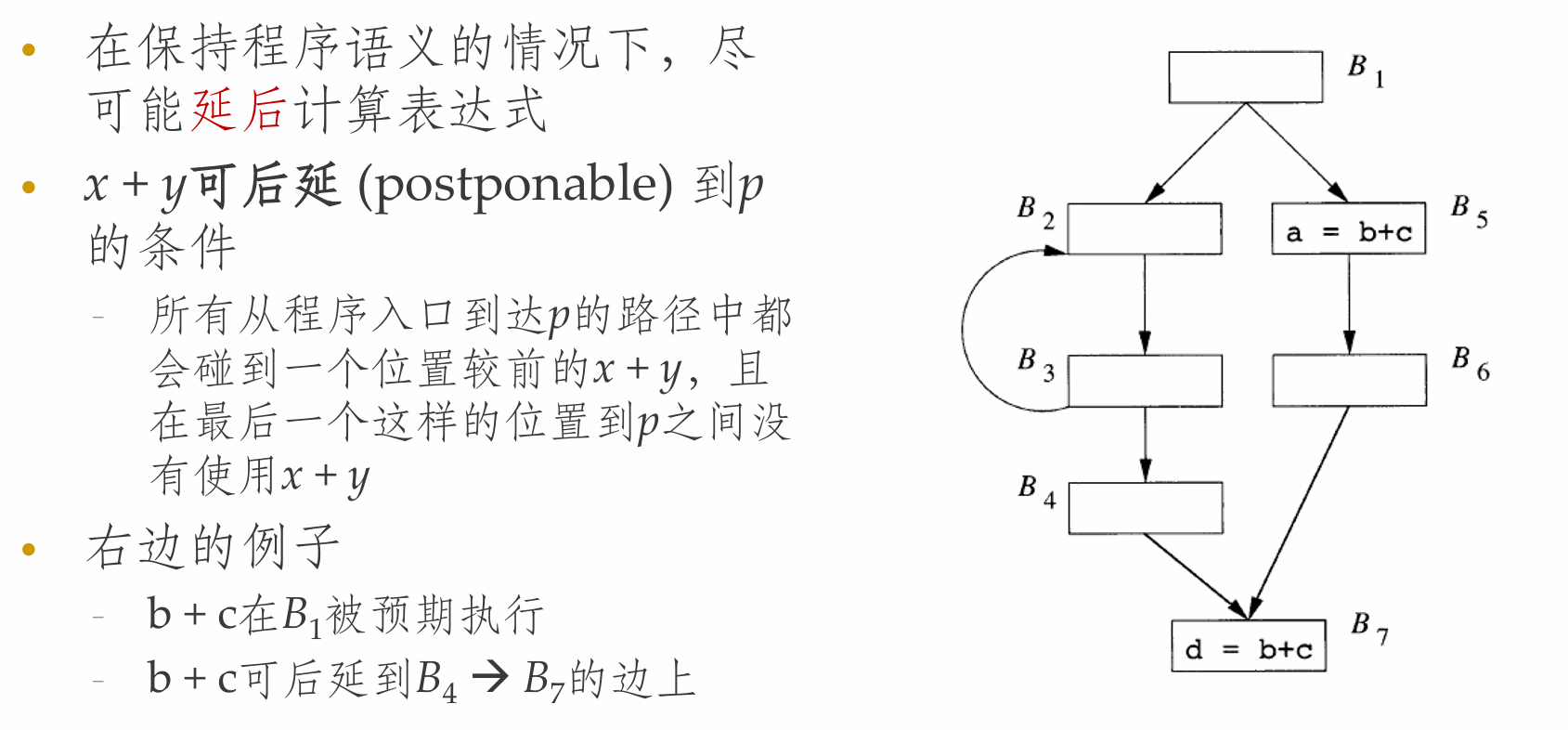
Tips:
粗略地说,一个表达式将被放置在边界上,即一个表达式从可后延变成不可后延的地方
Example:
被使用的表达式
- 确定一个被引入的临时变量是否在它所在基本块之外的其它地方被使用(used)
- 对表达式的活跃性分析
- 如果从程序点p出发的一条路径在表达式被重新求值之前使用了该表达式,那么该表达式在点p上被使用
流图中的循环
- 循环的重要性
- 程序的大部分执行时间都花在循环上
- 也是数据流分析需要经过若干次迭代的原因
支配结点
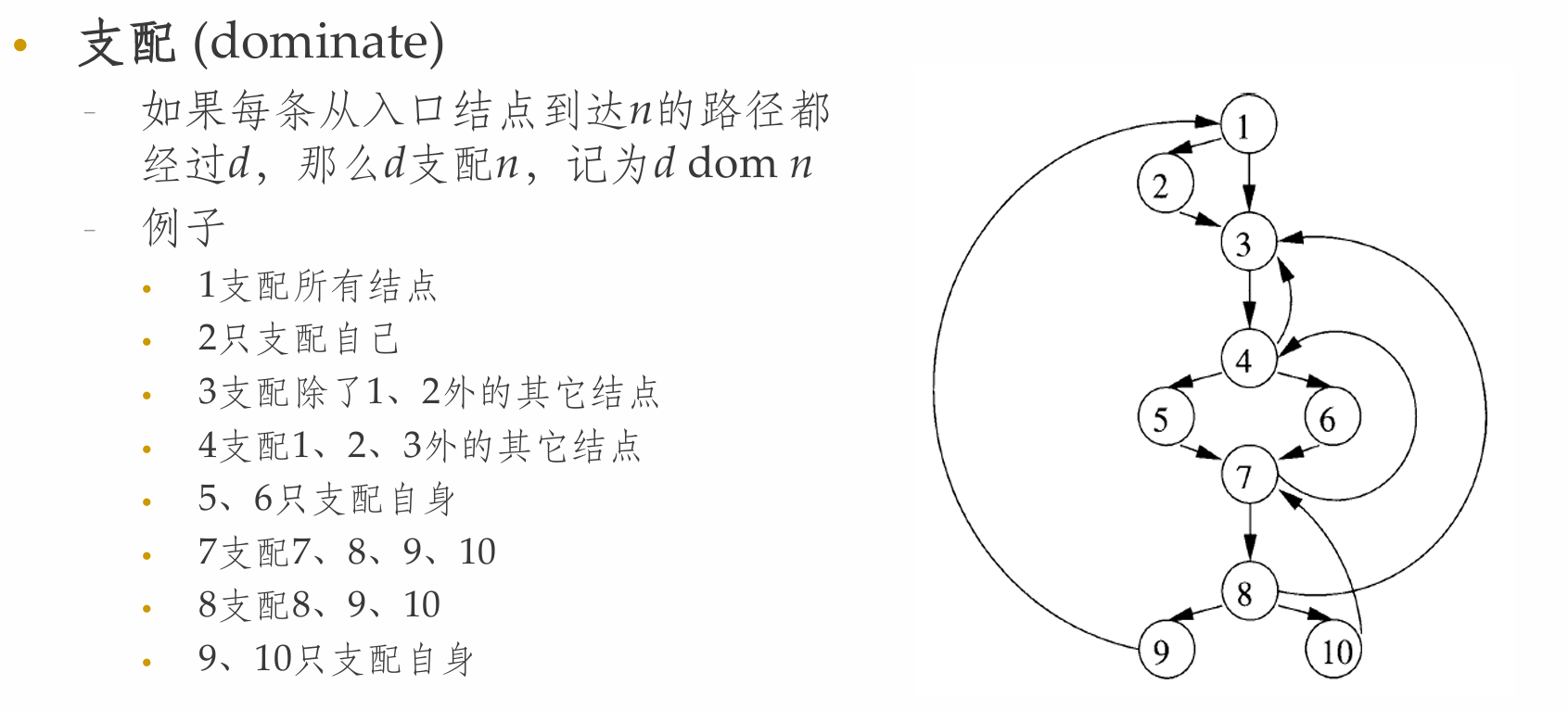
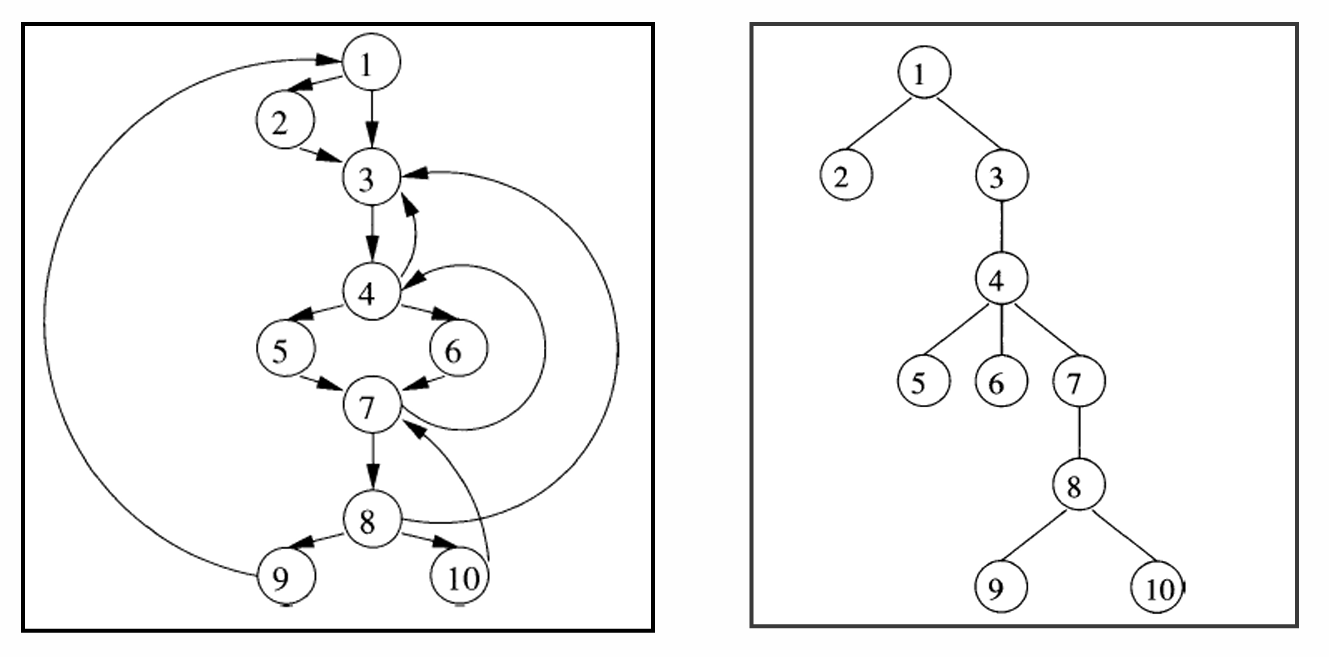
支配结点树
- 支配结点树(Dominator Tree)可以表示支配关系
- 根结点:入口结点
- 每个结点d支配且只支配树中的后代结点
- 直接支配结点(Immediate Dominator)
- 从入口结点到达
n的任何路径(不含n)中,它是路径中最后一个支配n的结点 n的直接支配结点m具有如下性质:如果d != n且d dom n,那么d dom m
- 从入口结点到达
Example: 支配节点树
寻找支配结点算法

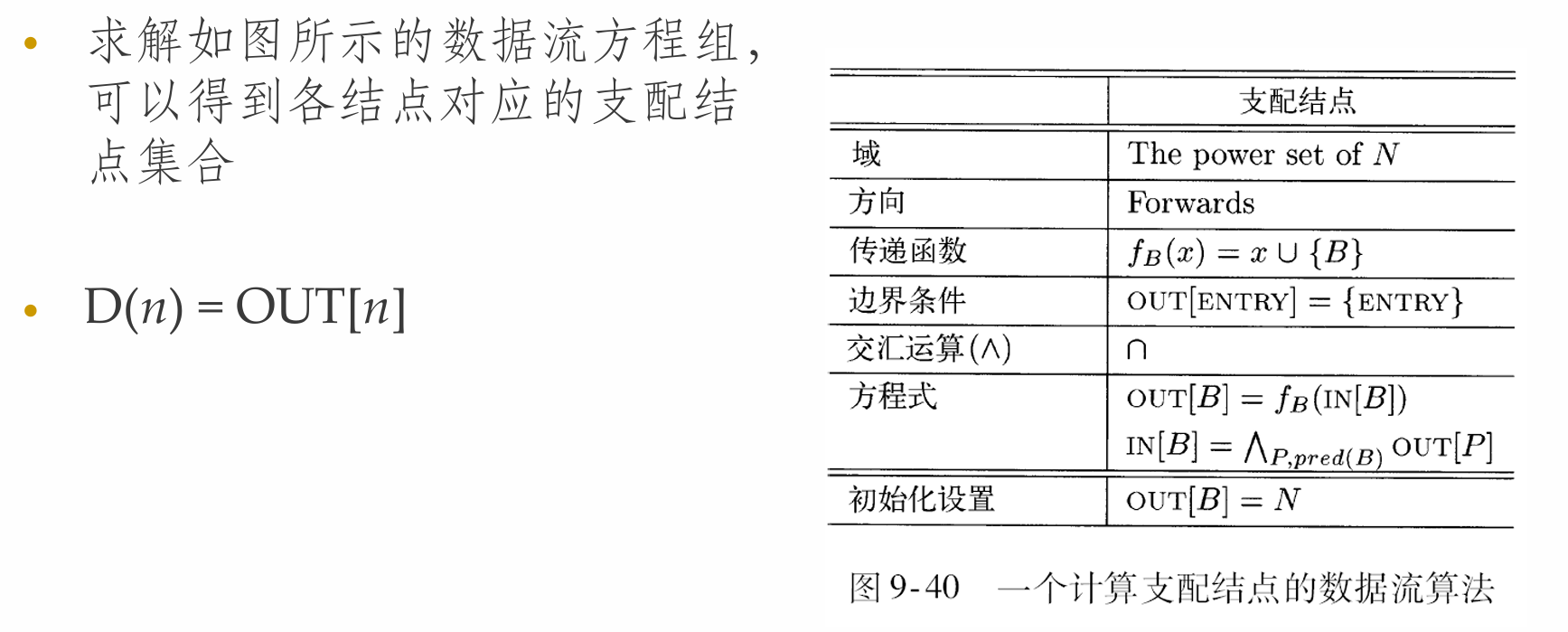
Example:
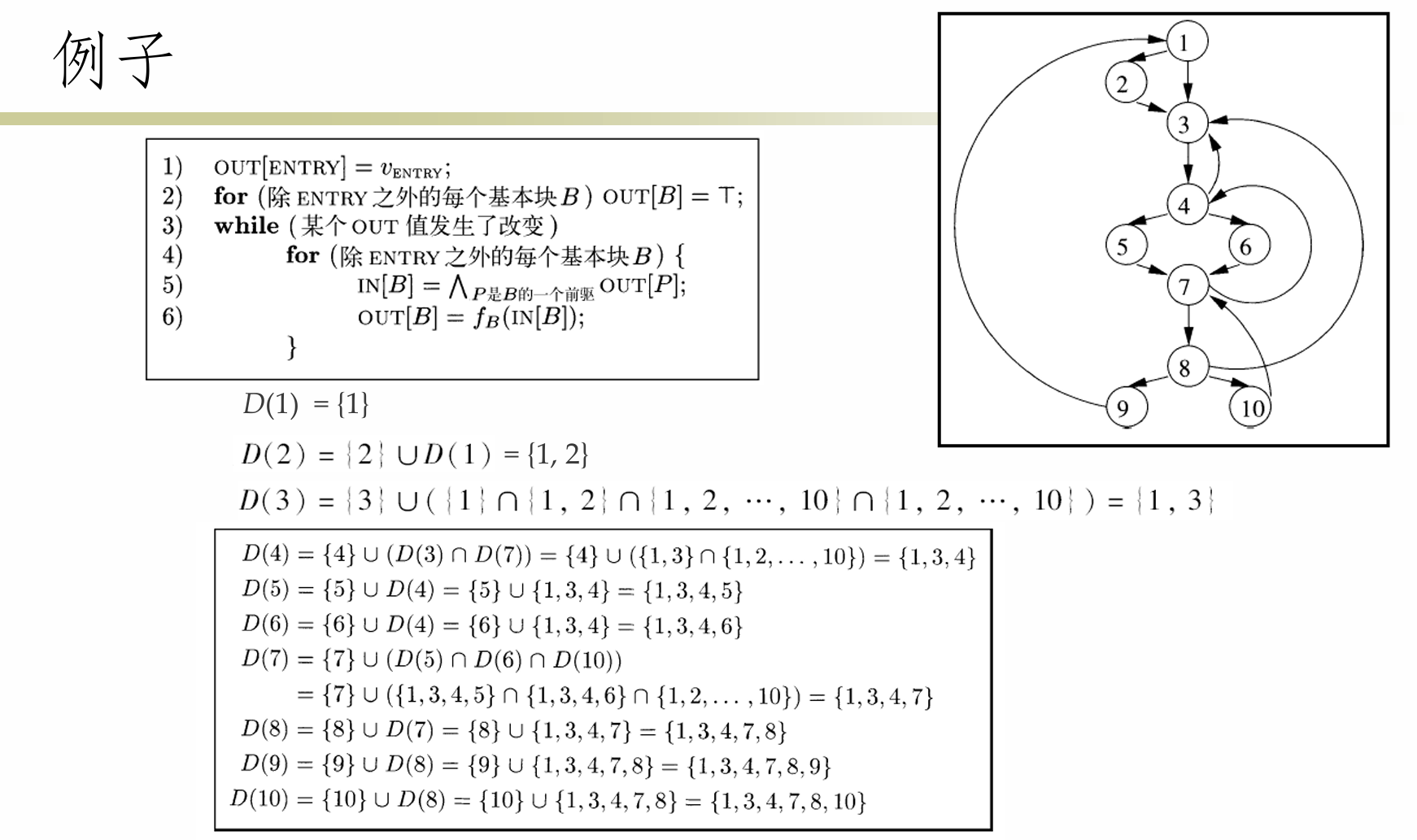
深度优先生成树
- 深度优先搜索(Depth-First Search)
- 搜索过程从入口结点开始,并首先访问离入口结点最远的结点
- 深度优先生成树
- 一个深度优先过程中的搜索路线形成了一个深度优先生成树(Depth-First Spanning Tree, DFST)
Example:
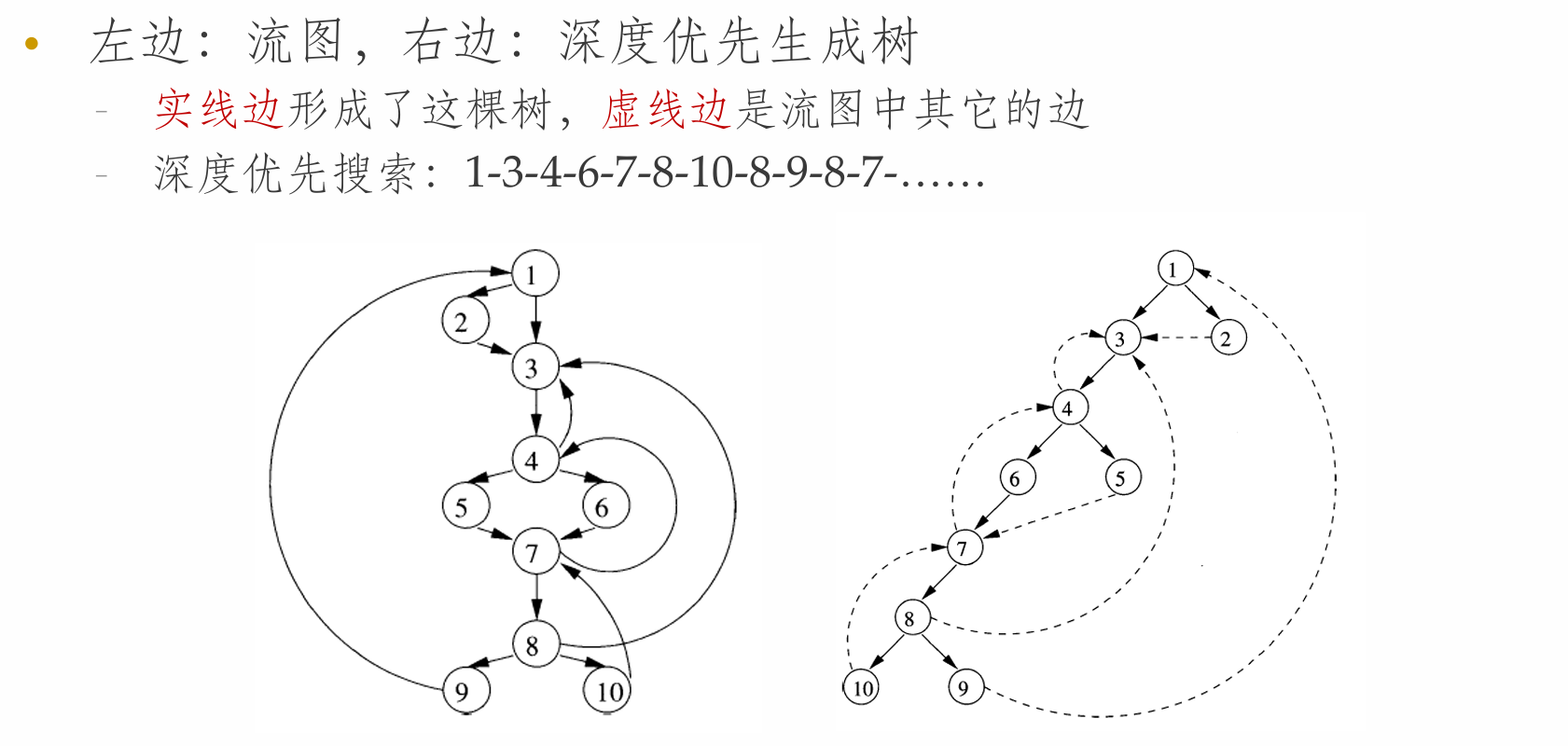
深度优先排序
- 前序遍历
- 先访问一个结点,然后从左到右递归地访问该结点的子结点
- 后序遍历
- 首先递归地从左到右访问一个结点的子结点,然后访问该结点
- 深度优先排序(Depth-First Ordering)
- 首先访问一个结点,然后访问该结点的最右子结点,再访问这个子结点左边的子结点,依次类推(与后序遍历的顺序相反)
Example:
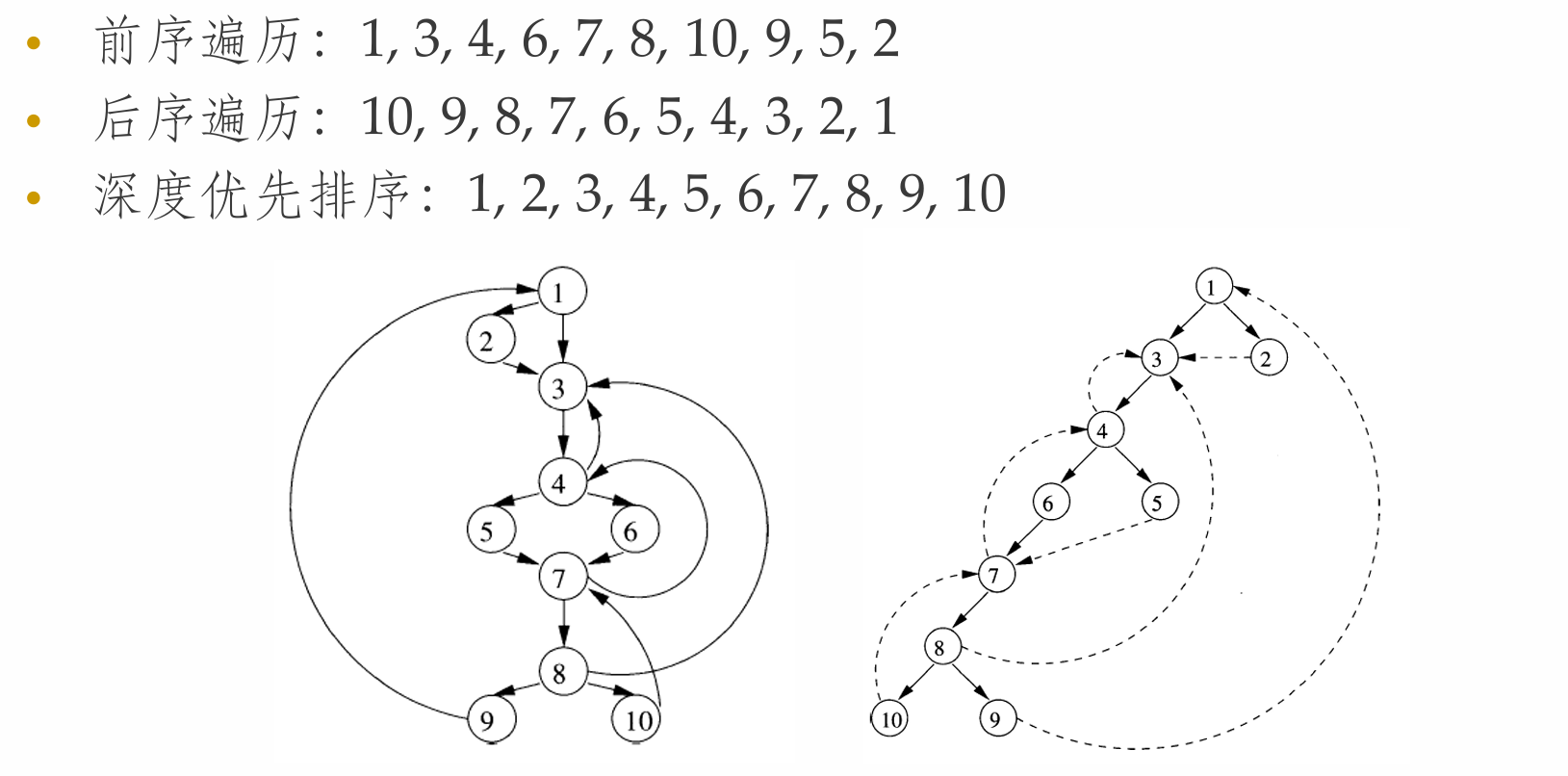
此处的遍历顺序是对于右边的深度优先生成树来说的
深度优先排序算法

流图中边的分类

回边和可归约性

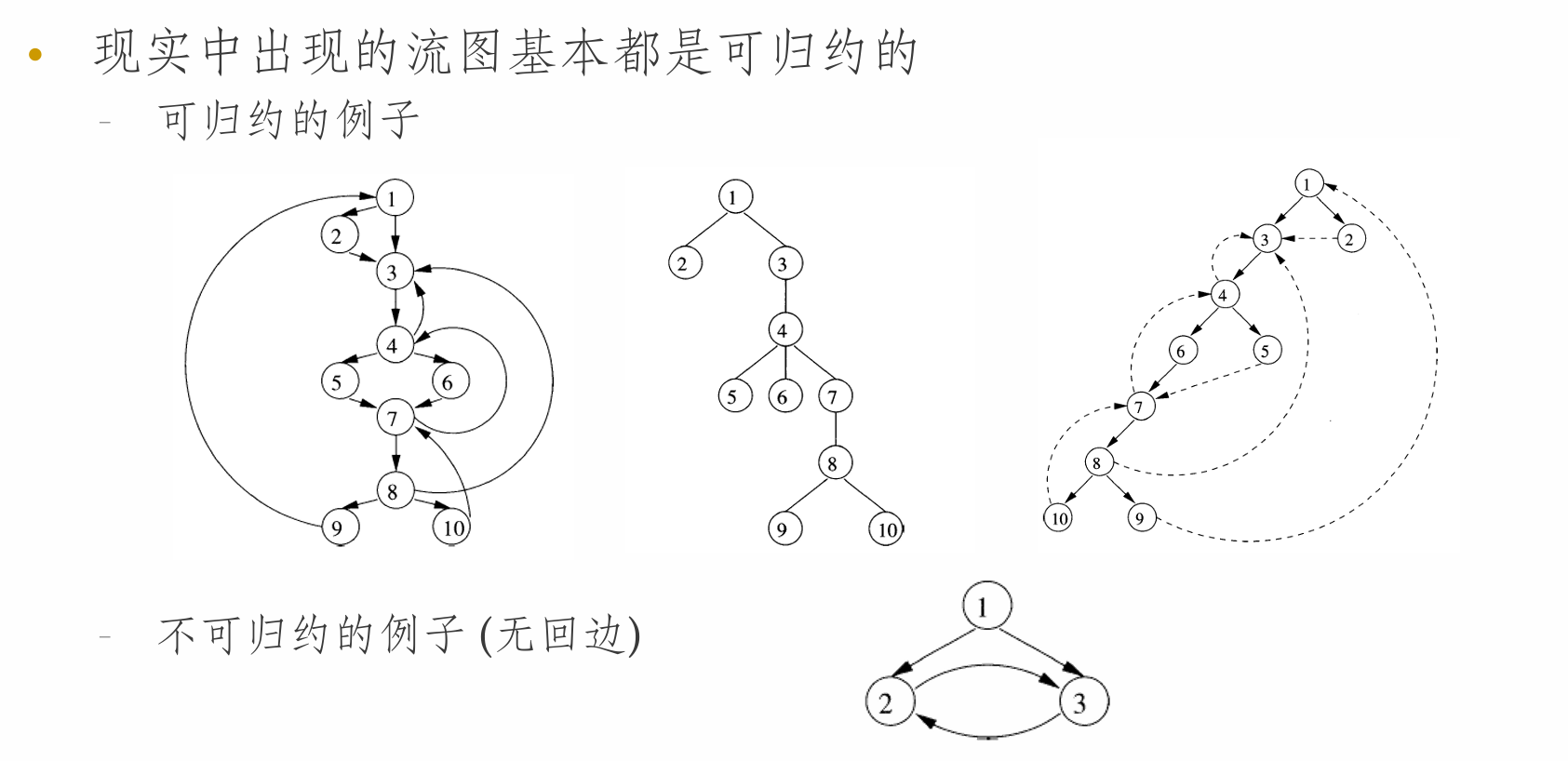
流图的深度
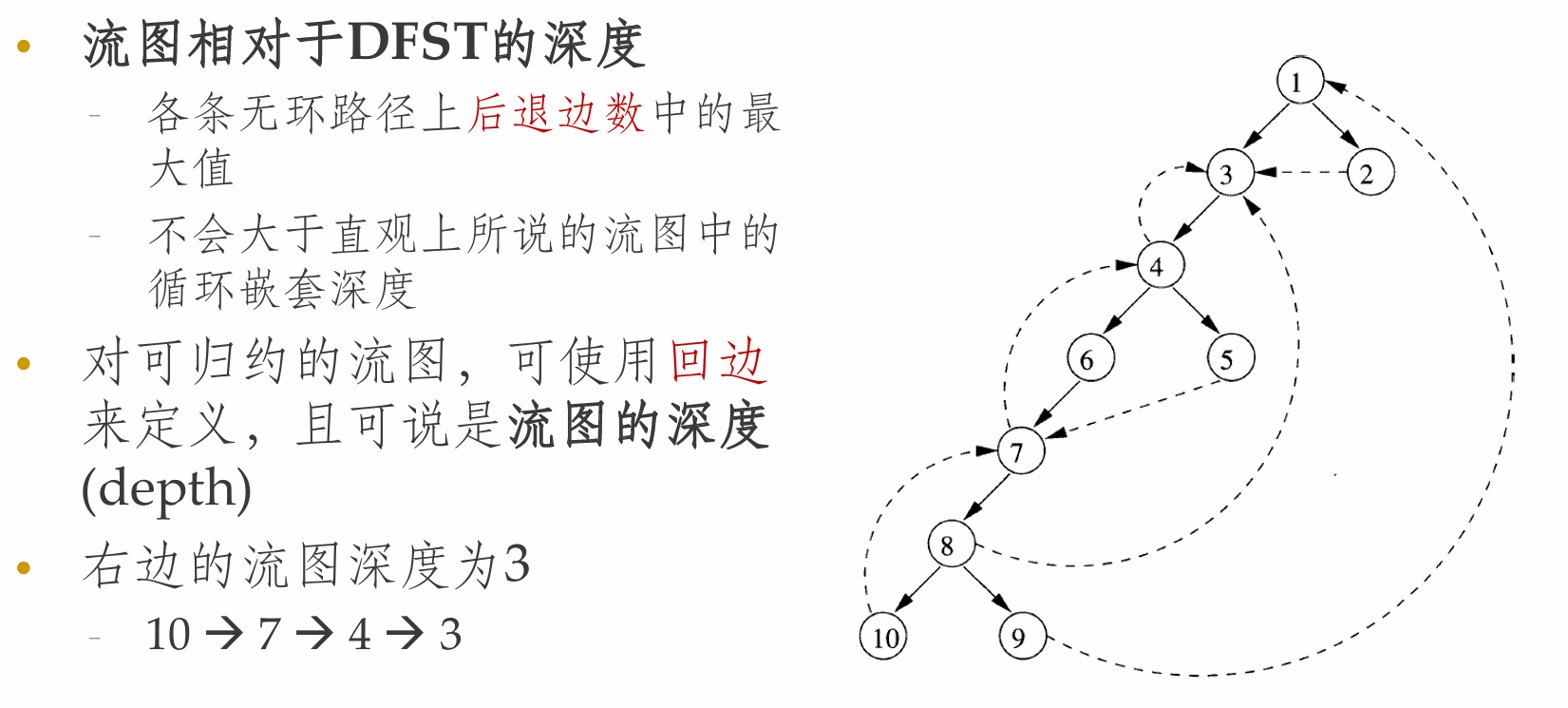
自然循环
- 自然循环的性质
- 有一个唯一的入口结点,即循环头(header),这个结点支配循环中的所有结点
- 必然存在进入循环头的回边
- 自然循环(Natural Loop)的定义
- 给定回边
n -> d的自然循环是d,加上不经过d就能够到达n的结点的集合 d是这个循环的头
- 给定回边
自然循环构造算法

Example:
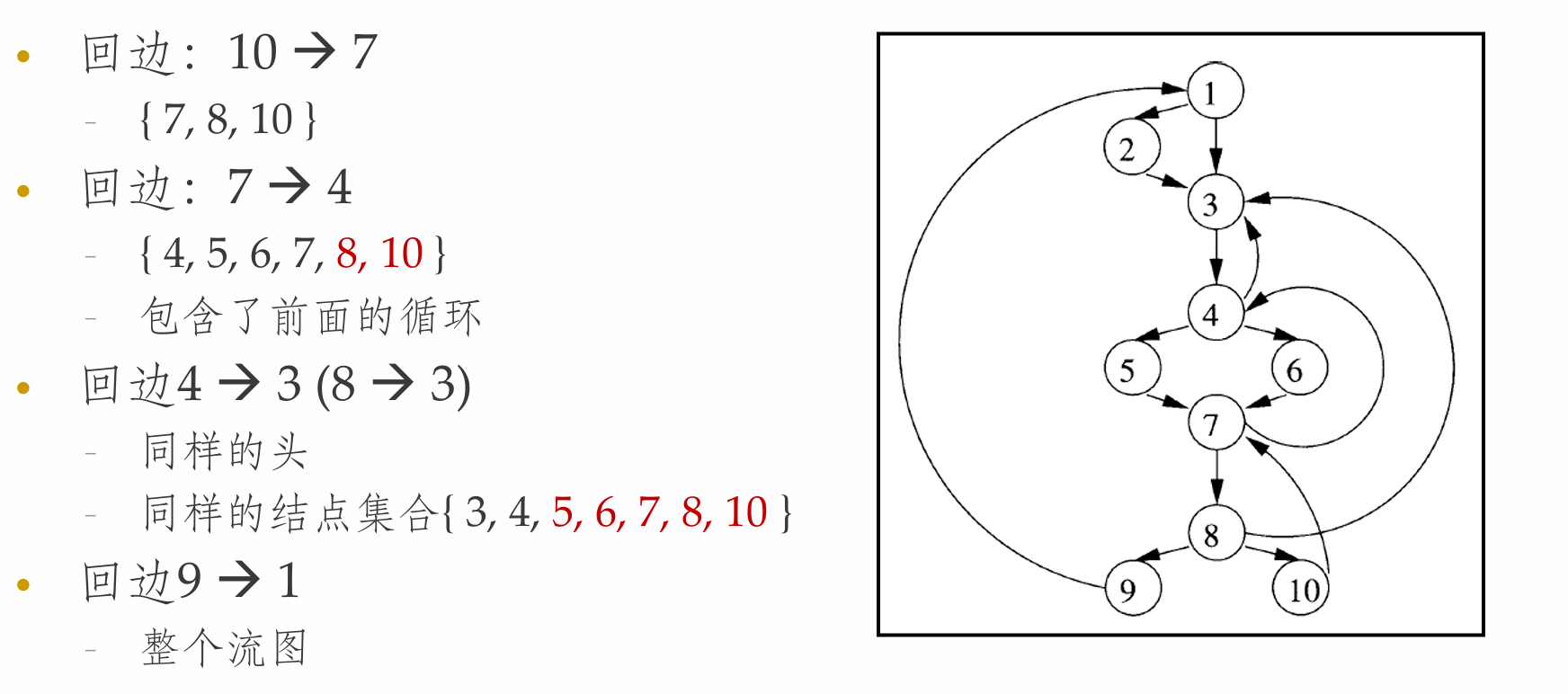
自然循环的性质

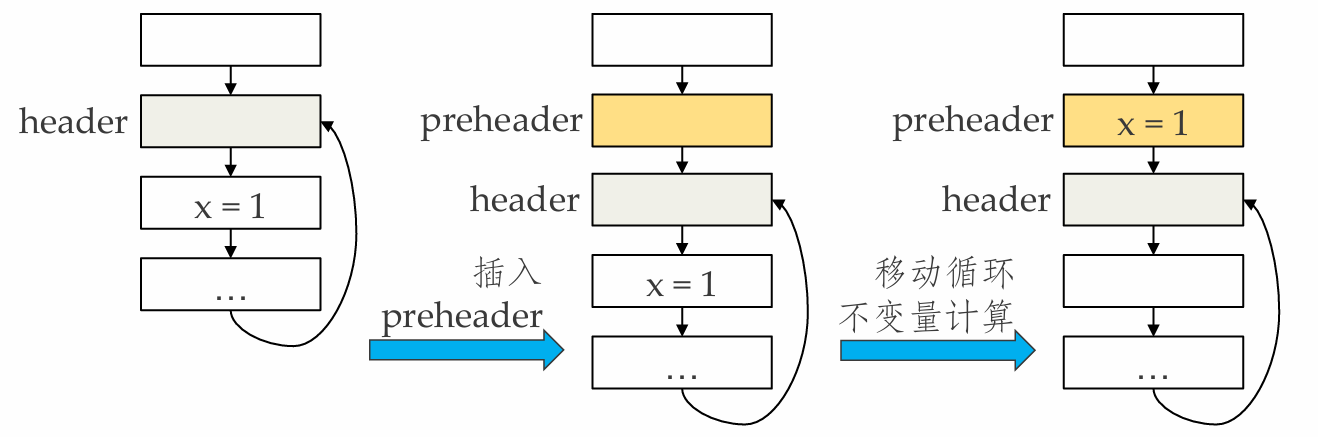
循环头上头(Preheader)
- 每个自然循环都有一个循环头header
- 一些循环相关的优化(如循环不变量移动)需要在循环头之前插入代码
- 常见做法是在循环头之前插入一个基本块(称为preheader),用于存放相关的代码