LaPluma

Keep it simple and stupid.

0%

NJU静态分析|A2-Constant Propagation

发表于 更新于 分类于 阅读次数：
本文字数： 5.2k 阅读时长 ≈ 9 分钟

NJU Static Program Analysis | Assignment-2 Constant Propagation & WorlistSolver.

实验信息与食用指南

请翻阅[NJU静态分析|A1-Live Variable Analysis].

在此进行一点补充, 笔者的这份实验记录更像是Free Style版的FAQ. 因此请 确保 在理解了理论知识, 实验指南 和 框架代码 后再参考本记录, 与A1相同, 本记录 不提供 源代码(或者说暂时没有).

如果您对本实验记录中的内容感到困惑, 可能是因为笔者能力不足或您未能理解实验指南和框架代码, 同时本试验记录难以涵盖所有的坑, 还望海涵.

实验目标

基于Tai-e框架实现常量传播算法和worklist求解器.

大致的框架代码如下:

注意常量传播算法是Forward & Must analysis.

部分重要框架代码带读

我知道你们有些人肯定是不看框架代码的, 除非不得不用或者报错的时候.

IR & IRBuilder

Tai-e框架中的IR与课上教授的IR稍有不同, 以A2 test中的Assign.java为例,

1
2
3
4
5
6
7
8
9
10
/*   From A2 test/Assign.java   */
class Assign {
    void assign() {
        int x = 1, y;
        x = 2;
        x = 3;
        x = 4;
        y = x;
    }
}

经过tai-e框架的分析后会得到

1
2
3
4
5
6
7
8
9
10
11
12
-------------------- <Assign: void <init>()> (constprop) --------------------
[0@L1] invokespecial %this.<java.lang.Object: void <init>()>(); {}
[1@L1] return; {}

-------------------- <Assign: void assign()> (constprop) --------------------
[0@L4] x = 1;   {x=1}
[1@L5] x = 2;   {x=2}
[2@L6] x = 3;   {x=3}
[3@L7] x = 4;   {x=4}
[4@L8] y = x;   {x=4, y=4}
[5@L8] return;  {x=4, y=4}

结合IR & IRBuilder(可翻阅[官方手册]),

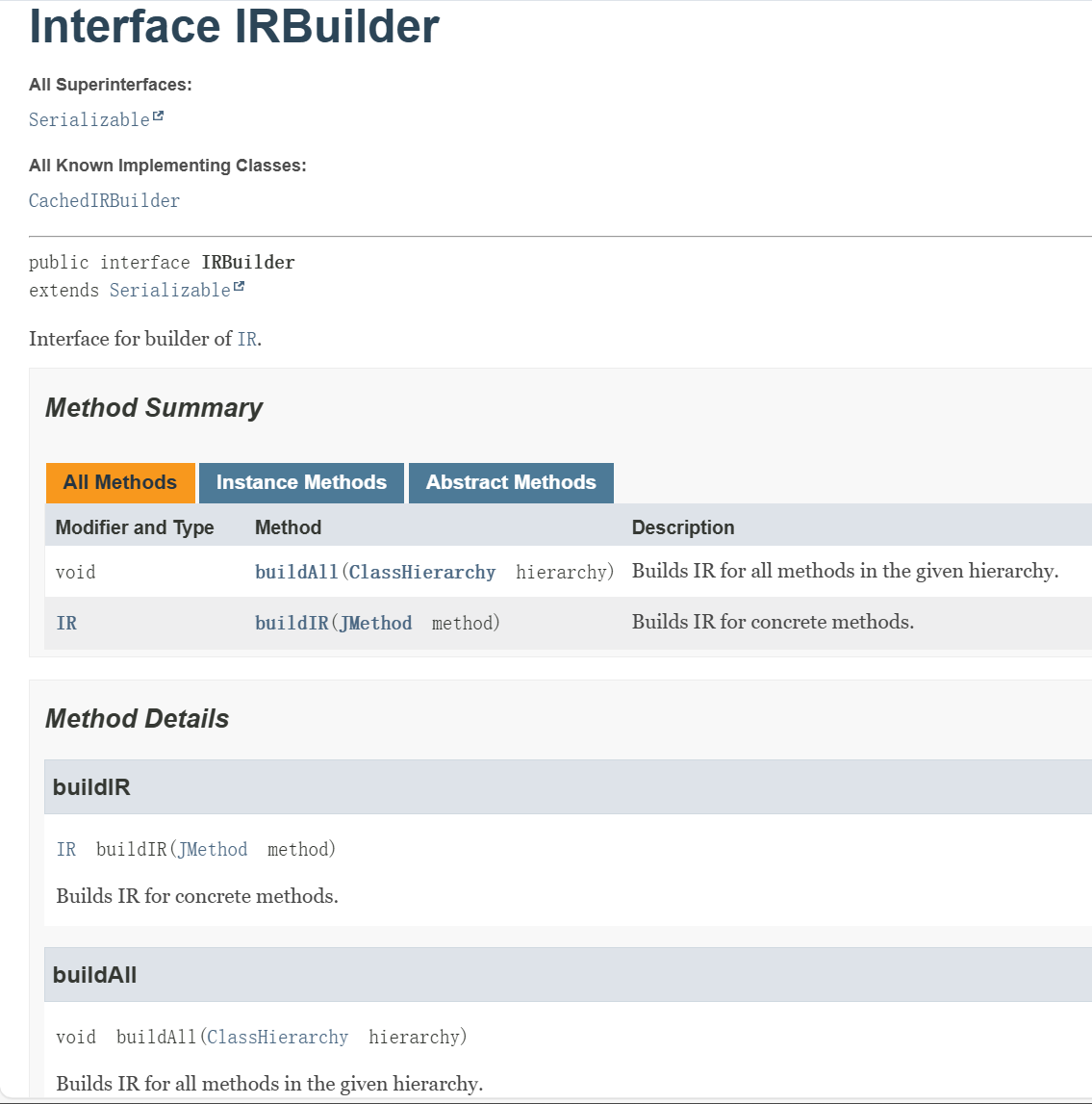
IR我懒得贴了

IR的基本单元是method (请意识到java是oop语言), IRBuilder提供了分析单个方法的APIbuildIR(JMethod method)和分析整个class hierarchy(不明白, 等到A4就明白了, 笑)中的所有方法的APIbuildAll()

结合Stmt Exp 和 CFG, 我们可以得到这样的一个示意图(由于笔者未阅读全部的源码实现, 可能会有所出入, 但大致如此).

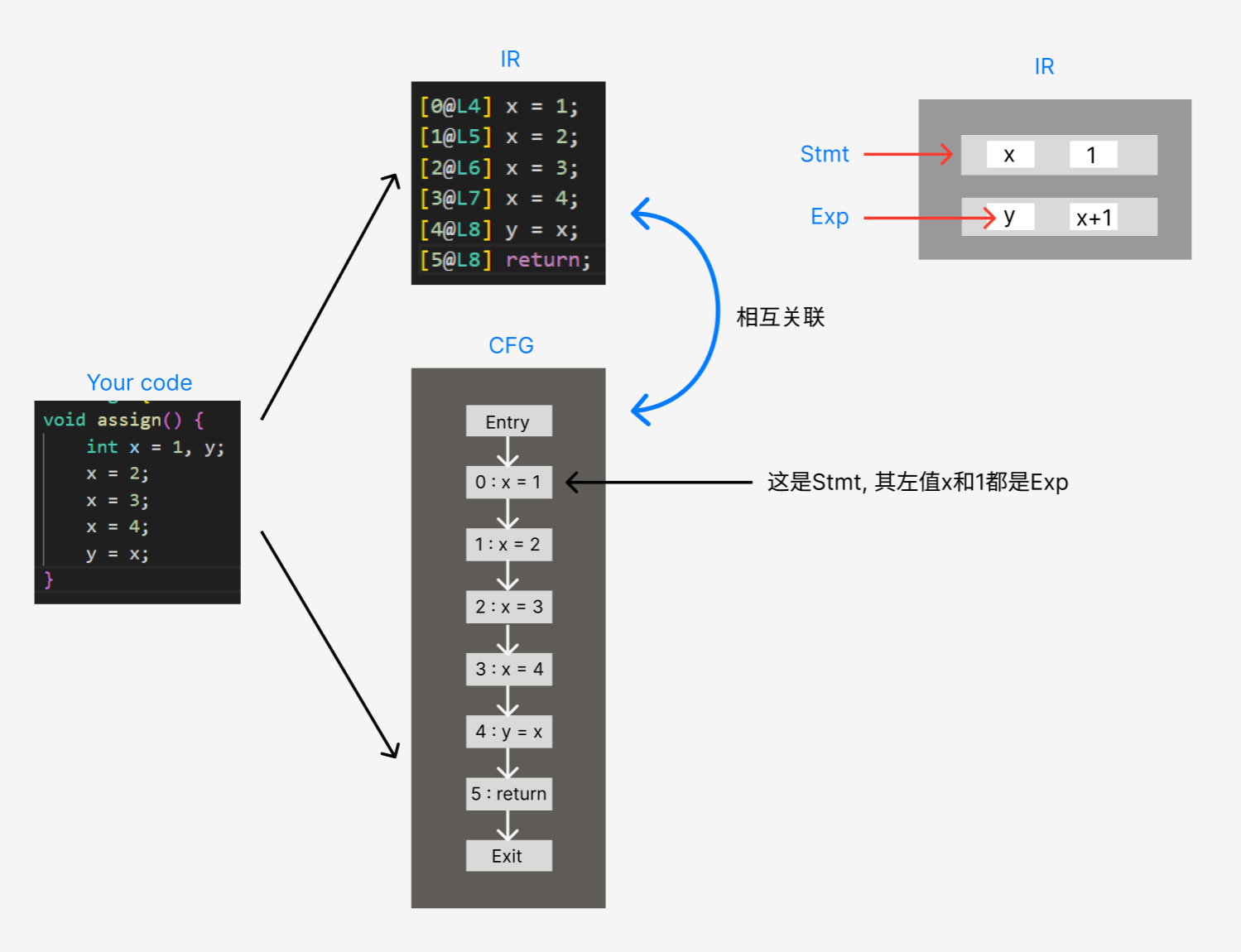
Tips: 严格来说CFG并不存储Node(本实验中指Stmt, 见A1试验记录说明), 只存储Stmt的关联信息, 但为了方便图示遂如此展示. 至于为何左值和右值都是Exp, 请翻阅A1官方实验指南中对Exp的图示表示部分.

DefinitionStmt

尽管理论上不需要这个类也可以完成实验(Stmt中的顶层方法足以实现), 但既然框架提供了这么好用的API, 方便我们写出更优雅的代码, 为什么不用呢?

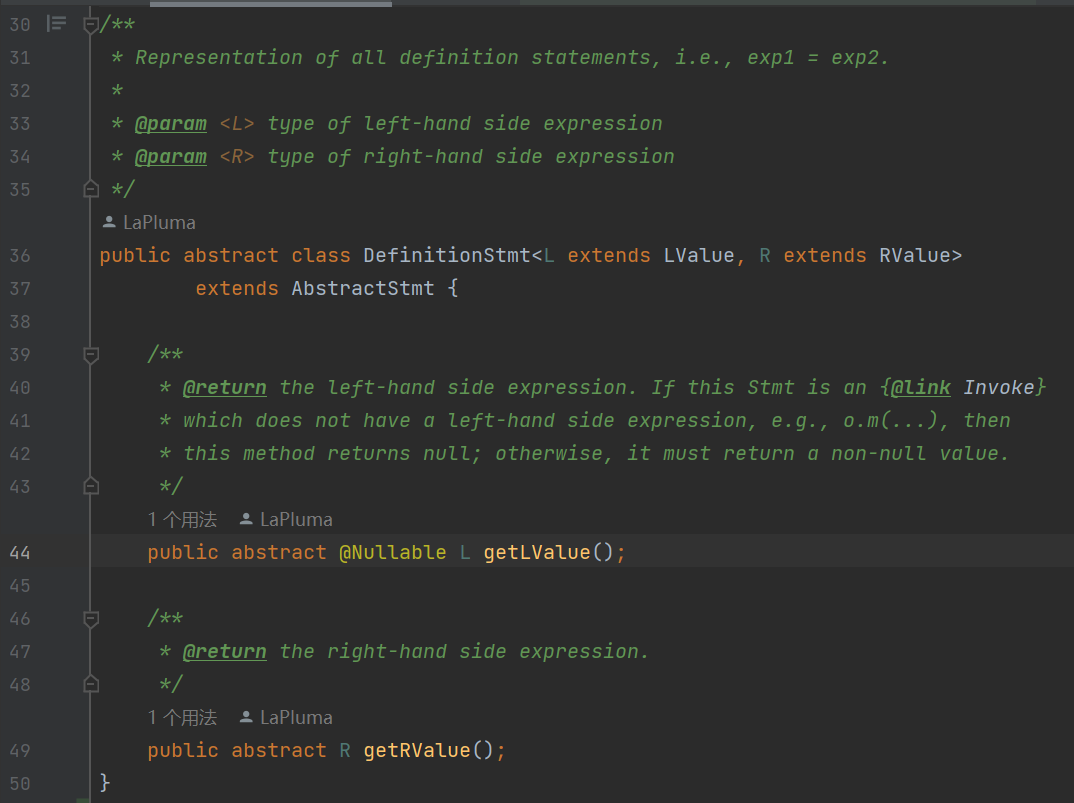
DefinitionStmt为我们提供了两个非常好用的API, getLValue()和getRValue可以直接获取到左右式的Exp(希望你还记得LValue&RValue extends Exp), 而不需要像Stmt中的getDef() & getUses() 做较为繁琐的判断和筛选(如果对getUses()感到困惑, 也还请翻阅A1实验记录, 里面有解释和参考来源).

需要注意的是, getLValue()可能会返回null.

ConstantPropagation

与活跃变量分析类似, 我们需要完成5个API的功能.

newBoundaryFact() & newInitialFact()

需要注意的是, 本次存储分析结果的数据结构是CPFact, 与A1相同, 在完成本次实验代码之前需要了解相关API的用法.

既然是Must Analysis, 我们需要将初值赋为空, 但需要注意的是, 我们的Analysis仅分析语句, 在进入第一条语句之前, 是否有什么东西需要初始化?

这个问题就对应了指南中为什么BoundaryInit 要通过 getIR().getParas()获取参数并赋值NAC的提示.

在对IR的解释中我们提到过, IR的基本分析单元是method, 即函数, 函数就可能有传入的参数, 这些参数易见不是Constant, 因此要赋值为NAC

Tips: 如果是Constant干嘛还要传参, 即便真的这么做了, 我们的分析也可以满足safe-approximation.

这部分是在方法体(函数语句)执行前就完成的初始化, 因此我们需要赋值给Entry的outFact.

meetValue() & meetInto()

meetValue()的完成没有任何难点, 只需要照抄ppt中的规则即可.

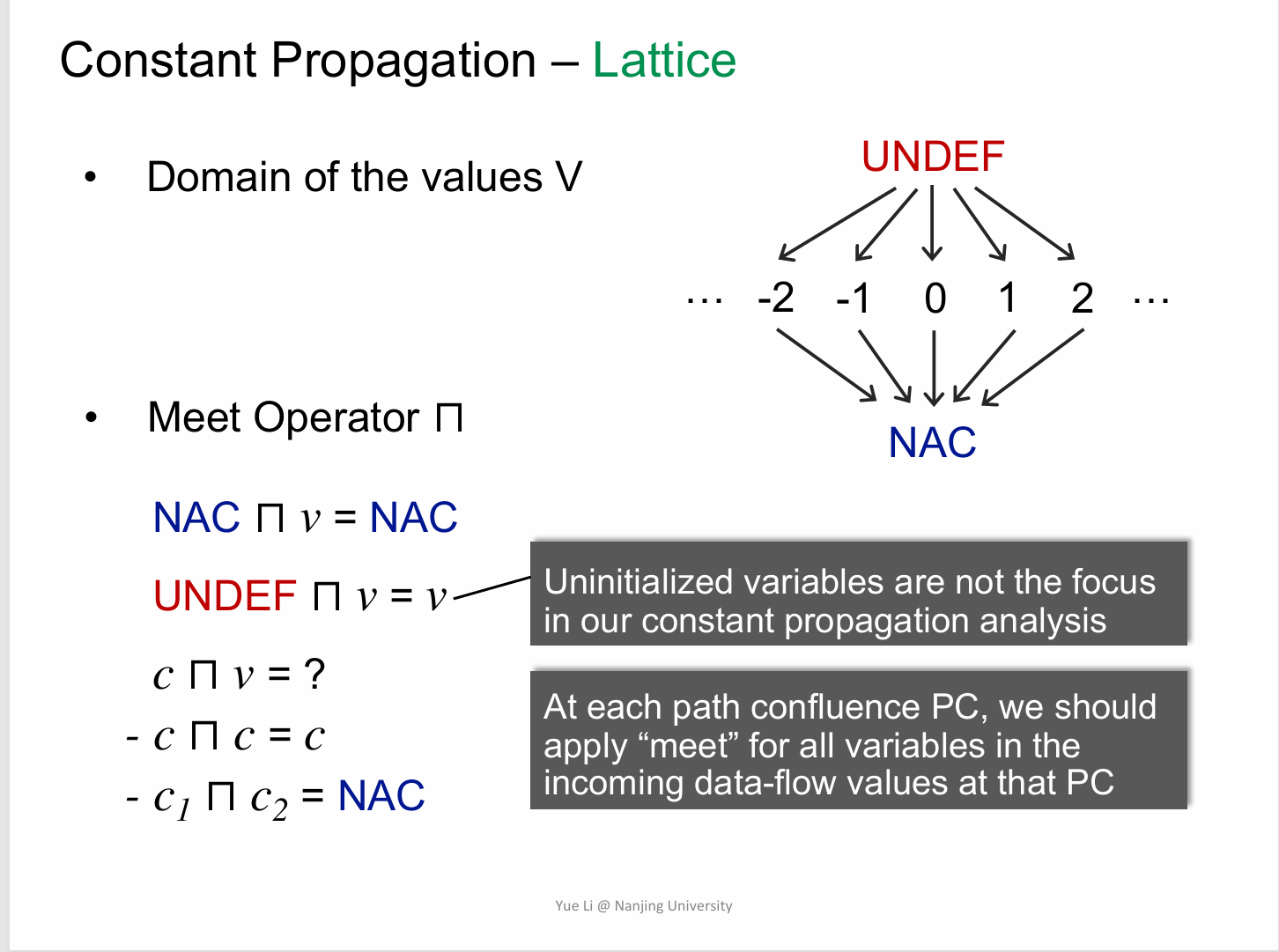
同样的, 完成这部分代码需要阅读Class Value的源码API和注释.

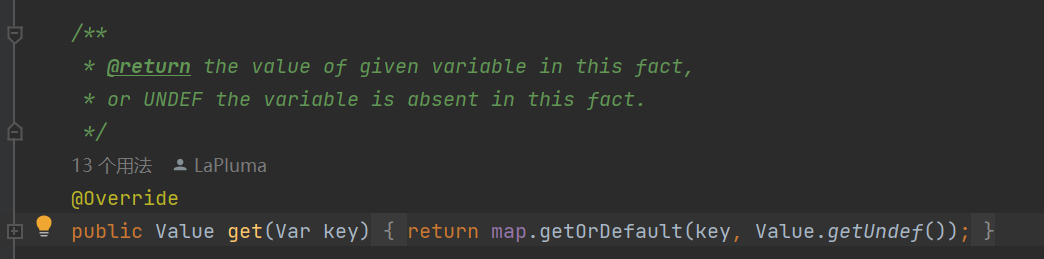
关于meetInto(), 如果没有阅读CPFact中的update()方法注释, 就不知道可以写出如此优雅的代码来合并Var的Value值:

1
target.update(var, meetValue(fact.get(var), target.get(var)));

transferNode() & evaluate()

毫无疑问, 这是本次实验中最难最核心的一部分, 细节非常多, 当被卡hidden test的时候, 大概率寄在这里.

笔者建议在transferNode()中处理Stmt的左值def部分, 在evaluate()中处理右值exp部分. 这是比较符合功能分离的写法, 当然, 也可以选择在 transferNode()中处理Var和IntLiteral, evaluate()只负责处理BinaryExp的计算值. 笔者在此按第一种写法进行说明.

transferNode()

这个函数中你需要依次做(次流程可能存在可以优化的部分, 不必完全照做):

  • 保存outFact原值, 将inFact赋值给outFact.

  • 判断Node(Stmt)是否为DefinitionStmt

  • 判断是否拥有合法左值, 包括def的类型Var和Var中的ValueType是否为Int, 如果不是, 本次实验中可以认为是nop空操作. 不需要为这个Stmt做任何分析, 直接将inFact copy给 outFact即可.

    Tips: IDEA教给我一个很有意思的语法糖

    1
    2
    3
    4
    if(stmt instanceof DefinitionStmt def_stmt){
        LValue def = def_stmt.getLValue();
        ...
    }

    这个用法可以避开繁琐的类型转化, 在判断类型时便做了类型转化.

  • 计算Stmt的右值(通过evaluate()获得), 并更新outFact中的相应Var def(笔者在此并未使用update方法的返回值, 或许可从此处入手优化效率, 但笔者不能保证其正确性)

  • 比较outFact是否更新返回布尔值.

evaluate()

为了完成这个方法, 代码的大致框架应该是这个样子:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
public static Value evaluate(Exp exp, CPFact in) {
    if(exp instanceof Var){
        ...
        return /*Value*/
    }
    if(exp instanceof IntLiteral){
        ...
        return /*Value*/
    }
    if(exp instanceof BinaryExp binary_exp){
        Value left = ...;
        Value right = ...;
        // Operand may not Int or may not Constant
        // you'd better do it first
        if(/*left HoldInt && right HoldInt*/){
            //you can get Condition Info form ppt
            if(/*left is Constant && right is constant*/){
                if (binary_exp instanceof ArithmeticExp arithmetic_exp){
                    ...
                    switch(op){
                        //also should attention to DIV 0 return Undef
                        case ADD: ...
                        ...
                    }
                }
                if (binary_exp instanceof BitwiseExp bitwise_exp){
                    ...
                    switch(op){
                        case AND: ...
                        ...
                    }
                }
                if(...)
                ...
            }
            else if(/*left is NAC || right is NAC*/){
                //you should do DIV & REM for 0 judgement there
                ...
            }
            else if(/*other condition*/){
                ...
            }
            else if(/*other condition*/){
                ...
            }
            ...
        }
        //for over-approximation
        return Value.getNAC();
    }
    //such as x = o.f()
    //for over-approximation
    return Value.getNAC(); 
}

其中二元表达式计算规则见ppt所示,

笔者在此给出一些细节和边界条件, 也可以通过阅读上述代码框架获得细节提示:

  • exp中的操作数可能不是IntType, 所以你需要做一个canHoldInt()判断, 非法exp为了安全性应赋值为NAC

  • 实验指南中提到, 对于/和%的除零错误, 应当给出Undef, 即使被除数是NAC.

Sovler & WorkListSolver

Sovler Init

照着算法流程前三行写便是, 但这里要提到框架代码的"robustness".

尽管从分析流程上来看, 我们不应该分析Node Entry, 但是框架代码允许我们这样做. 这时框架代码会认为Node Entry是一条nop Stmt, 不会做constant update, 因此只要在Init部分对Entry的inFact和outFact都赋上初值, 就不需要在worklist中考虑Entry的处理了.

WorkListSolver doSolveForward

worklist是一种非常简单的算法, 笔者在此不对算法实现过多赘述. 注意在实现worklist的时候可以使用java自带的容器Queue & ArrayList.

关于worklist的初始化问题, 需要注意的是应当为其加入所有的Node, 如果只加入Entry的后继, 会产生问题, 笔者在此给出一个例子. (感谢课程群中日居月诸大佬和另一位不知道github链接的大佬构造的反例)

1
2
3
4
5
6
7
8
9
-------------------- <Assign: void assign()> (constprop) --------------------
[0@L4] nop;     {}
[0@L4] x = 1;   {x=1}
[1@L5] x = 2;   {x=2}
[2@L6] x = 3;   {x=3}
[3@L7] x = 4;   {x=4}
[4@L8] y = x;   {x=4, y=4}
[5@L8] return;  {x=4, y=4}

在这个例子中, Entry outFact初始化为{}(没有参数), 然而Stmt0 的 outFact 同样初始化为{}, 如果只添加Entry的后继{Stmt0}, 会导致worklist在分析完Stmt0后错误终止.

总结

本次实验应该是所有Assignment中代码量最多的一次, 细节也是让人头皮发麻, 还望能静下心来看代码和debug, 祝早日AC!