LaPluma

Keep it simple and stupid.

0%

NJU静态分析|A7-Alias-Aware Interprocedural Constant Propagation

发表于 更新于 分类于 阅读次数：
本文字数： 6k 阅读时长 ≈ 11 分钟

NJU Static Program Analysis | Assignment-7 Alias-Aware Interprocedural Constant Propagation.

实验目标

基于tai-e框架实现带别名分析的过程间常量传播.

Preparation

  • 将A2/.../ConstantPropagation复制到A7/.../ConstantPropagation

  • 将A4/.../InterConstantPropagation复制到A7/.../InterConstantPropagation

  • 将A4/.../InterSolver复制到A7/InterSolver

  • 将A6/.../cs/Solver复制到A7/.../cs/Solver

  • 将A6/.../_2ObjSelector复制到A7/.../_2ObjSelector

    Tips: plan.yml已经配置好了cs: 2-obj, 如果本地测试中想要使用其他策略, 需要将对应Selector复制到本次实验目录, 并配置plan.yml(方法已在A6实验指南中给出)

注意: 除去指针分析的部分作为结果查询字段指向外, 其余文件都可以是本次实验的更改范围.

Review

由于要设计算法, 不妨先复习一下A2和A4中常量传播算法和应用范围.

  • 常量传播算法是Forward & Must Analysis. 迭代至收敛至"最大"不动点.

    Additional:

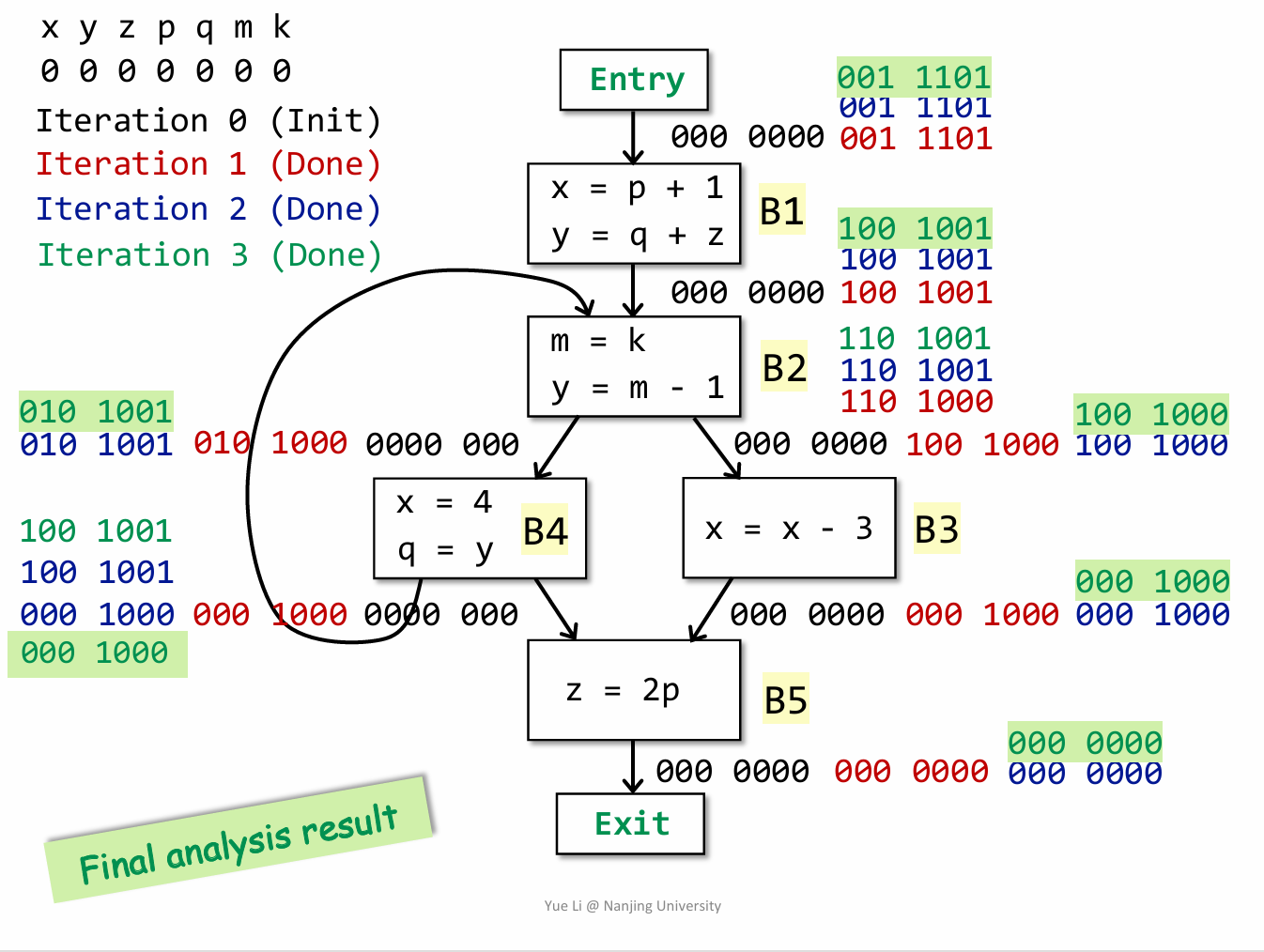
    迭代算法框架如下:

    活跃变量分析的迭代示例:

  • 常量传播算法中对数值的抽象为UNDEF->CONST->NAC.

  • 由于数据流动的"单调性", Meet要满足

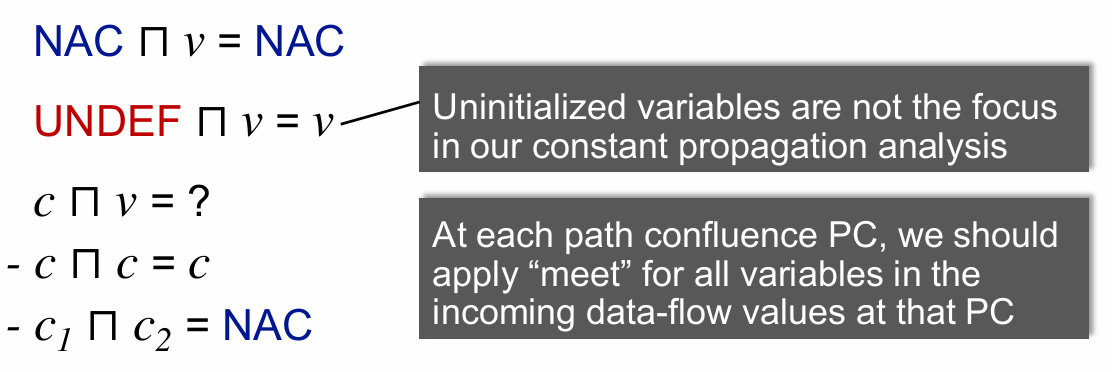
  • 语句处理的Transfer Function

在A2中, 处理范围仅限于DefinitionStmt中的变量和表达式部分, 对于诸如字段, 数组部分采取保守策略, 赋值为NAC; 分析范围仅局限于过程内分析, 此时为方法调用的返回值采取保守策略, 赋值为NAC.

在A4中, 同样只处理变量, 但分析范围扩展为过程间分析, 需要完成对方法调用传参, 传返回值, 为了完成过程间的数据流传递, 加入了Transfer Edge.

由于方法调用的动态时确认, 需要知道在这个调用点callsite, 真正的callee是什么, 因此建立CallGraph为ICFG(inter-procedural control-flow graph) 提供调用图信息.(你应该还记得在A4的CHABuilder完成前, Assignment不会输出任何ICFG信息)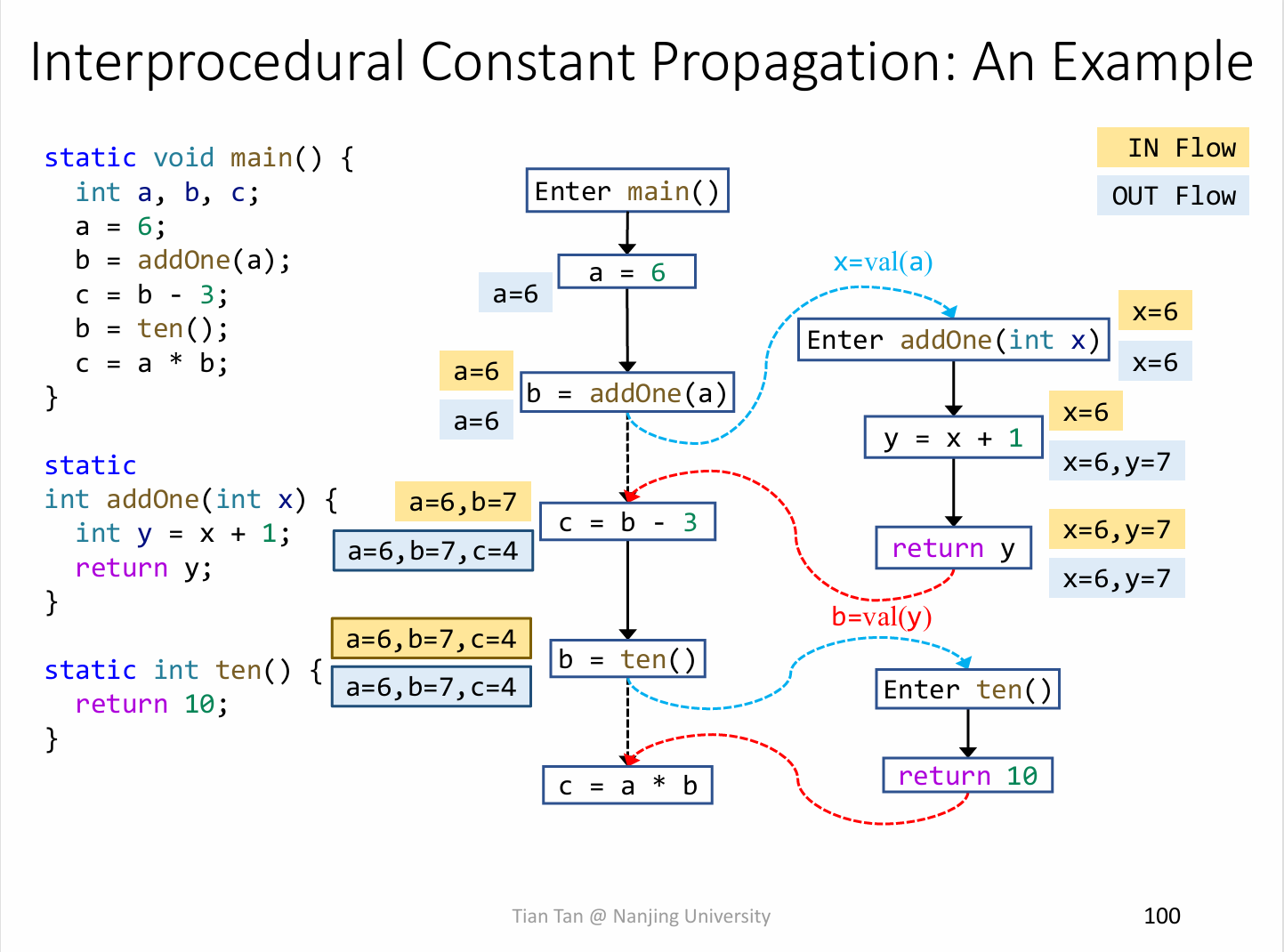

Requirement & Analysis

现在来看看实验要求和手上的工具, 看看如何处理新需求.

常量处理范围

在之前的实验中, 忽略了字段Field和数组Array的分析, 原因在本次实验已经指出, 是别名Alias所引起的, 由于多个变量(指针)可以指向同一个对象, 只有当明确指针所指向对象时, 才能为其赋值常量Constant.

需要指出的是, 本次实验仍然只需要处理int类型的变量. A2中已经提供了足够好用的canHoldInt().

另外, 指南上讲述了实验框架中会忽略静态字段的初始化的情况, 因其在控制流图中不可达, 不需要对其进行额外的处理.

域分析范围

A4开始采用了一种精度较低的方法CHA构建CallGraph; A5, A6使用了精度更高的指针分析技术构建CallGraph.

本次实验仍然是处理过程间常量传播, 由于CallGraph更加精确, 分析精度相较于A4也会更进一步. 同时, 在Tai-e框架下完成实验不需要关注ICFG如何获得CG信息(如有兴趣可自行阅读框架代码).

PointerAnalysisResult

框架代码提供了class PointerAnalysisResult用来获取指针分析的结果, 该部分的初始化在InterConstantPropagation中的initial()中完成.

其中包含的API说明都较为清晰, 笔者在此不过多赘述.

别名分析

该部分实验指南已经给出了一个比较简单的实现方法, Pointer指向的PointsToSet存在交集, 则认为二者互为别名.

换个说法, 存在两个或两个以上Pointer指向同一个Obj, 则认为二者互为别名.

实验指南中讲述了为什么只需要Pointer而不是CSPointer的原因

笔者在此给出两个简单的算法思路:

  • 遍历所有的Pointer1与Pointer2, 获取PointsToSet, 如果有交集就加入Multiple Map中, 简单地以<Var, Var>的形式维护alias信息.

  • 遍历所有的Pointer和对应的PointsToSet, 维护一个<Obj, Var>结构, 对于<Obj, Var1>和<Obj, Var2>, Var1和Var2互为别名.

Tips: 框架代码的做法

如果你有阅读过框架代码或者"意外"跳转到class Maps, 便会发现, Tai-e框架中已经配置了好了获取基本数据结构的API(被TT深不可测的代码力所折服). 可以通过简单的Maps.newMultiMap()获取实例化数据结构. 当然, 也可以选择自己实例化Map的结构.

不过需要注意的是, 该部分代码不是显式给出的, 而是封装在tai-e-assignment.jar中, 可以选择阅读科研版doc或者阅读反编译后的源码(该部分结构简单, 即便无注释也可以理解)

Field处理

在这里会遇到第一个头疼的点: ConstPropagation是流敏感的, 但PointerAnalysis是流不敏感的.

尽管别名信息不依赖于常量传播, 但对象存储的值来源常量传播. 因此, 需要先理清楚如何处理Load和Store.(注意: 笔者以下论述基于InstanceField, SaticField的处理只会比InstanceField简单)

Try: 先收集所有的Store再更新给Load?

这是符合流不敏感的思路, 但是在ConstPropagation的流敏感框架中非常难以实现. 在迭代过程中, Store的右值可能会改变, Store的变化也会引起非Field和Array变量的变化. 所以, Field和Array的更新也需要采用流敏感框架中的迭代方法.

现在来分析如何用迭代的方法处理Field.

  • 对于Load, 因为迭代的缘故, 可以先假设后续的处理会正确的广播到此处, 更新Load的值. 因此只需要简单的传播到def即可.

  • 对于Store, 假设已经有了一个对应的Load结构, Store产生了更新该如何广播? worklist加入Load Stmt迭代即可.

  • 同时, 需要注意InstanceFiled的特性, 考虑别名信息进行更新即可.

Array处理

Array可以理解成一种特殊的InstanceField, 不过需要注意何时互为别名, 只有在互为别名的情况下才考虑广播.

小结

至此已经有了一个对完成本次实验的一个基本思路了, 接下来开始考虑一些完成实验的细节.

算法设计

Tips: 笔者在此章节不详谈实现上的细节, 该部分在拾遗章节分点给出. 并且, 由于框架代码的特性, 算法的实现可能与思路有所出入.

Question: 这次新写的代码和A4冲突吗?

这个问题实际上是在问: Field和Array的传播是否会影响到过程间常量传播的EdgeTransfer.

答案自然是否定的, Field和Array可以理解成一种特殊的Var, 尽管其结果不需要呈现在DataFlowResult中. 可以自然地得出结论: 加入Field和Array并不会改变A4的算法框架.

也即, 本次实验所设计的算法是对TransferNonCallNode(A2-IntraConstPropagation)的补全.

所以, 本次算法的基本框架可以表示为:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
boolean transferNonCallNode(Stmt stmt, CPFact in, CPFact out){
    if (stmt instanceof LoadField){
        //handle
    }
    if (stmt instanceof StoreFiled){
        //handle
    }
    if (stmt instanceof LoadArray){
        //handle
    }
    if (stmt instanceof StoreArray){
        //handle
    }
    else{
        cp.transferNode(); //form A2
    }
}

当然, 你也可以选择将这些语句的处理直接整合进ConstantPropagation(前提是A2的实现最好确保是正确的).

Tips: 还记得在A5和A6中是如何优雅地处理繁杂的instanceof判断吗? 对, 就是访问者模式, 在本次实验中, 仍然可以选择这样的方法实现算法. 所有的Stmt类中都已经内置了accept()API可供访问, 只需要新的访问类继承自StmtVisitor即可.

<Field, Value>的存储和广播

Tips: 在Tai-e框架中, 将Array等效抽象成Field, 并不对Index做具体的区分(对a[i]和a[j]的store操作视为对同一对象a[...]的store操作). 尽管如此, index信息也有助于分区a[i]和a[j]是否为别名, 从而决定是否需要广播. 因此, Array的维护会比Field更复杂, 但基本原理一致, 笔者在此章节不再赘述Array应如何处理.

在之前的分析中已经获知了Alias信息, 该部分算法的实现依赖于别名信息.

笔者在此给出两个算法思路抛砖引玉:

只考虑Alias层

这是个朴实但简单的想法: 所有的y = x.f来自也只来自x.f = z, 这句"废话"意味着什么?

意味着其实根本就不需要考虑x.f或者说oi.f的取值, 如果想知道y可能的value值, 只需要meet所有的z就可以了.

根据这个思路, 有:

  • 对于LoadField, 找到所有与x.f相关的x'.f = z, 其中x'是x的别名, meet z的value值. 如果y = meet(foreach(z))有更新, 将其后续Node加入workList.

  • 对于StoreField, 找到所有与x.f相关的y = x'.f, 其中x'是x的别名, 将这些StoreField加入workList.

这个算法的优点是实现简单, 但缺点是效率低, 展现着独属于暴力的美学魅力.

其关键在于如何维护<Field, Stmt>的结构, 框架代码中有不少细节需要关注.

考虑Map<Obj, Value>

x.f中的x是Pointer, 真正存储Value值的是Obj, 因此可以考虑维护<Var, Obj>和<Obj.field, Value>两个Map, Load和Store均对Map进行操作.

该思路避免了之前算法中的大量冗余计算(笔者自测跑完本地测试需要近30s), 提高了效率, 但Map的维护较为复杂.

具体处理LoadField和StoreField时, 只需要将信息更新到Map<Obj.field, Value>即可, 广播逻辑与之前相同.

不过需要注意的是, 由于指针分析结果是流不敏感的, 对于Store操作只使用meet而不是kill.

Question: Store语句应该在何时广播?

答案是当outFact改变的时候广播, 或者具体来说,是x.f = y的y的value值改变时进行广播.

拾遗: Tai-e FAQ You Need to Know

CS & CI Pointer Analysis

CallGraph建立的ICFG是没有上下文的, 这和常量传播不关注上下文的行为一致. 但对Pointer指向信息可以使用带上下文的分析结果以获取更高的精度, 这与ICFG并不冲突.

IR

IR的使用为本次实验做了大量简化, 你可能会疑惑, 对于x.f = y.g这样的操作, 上述算法框架可以覆盖到该语句吗?

实际上, x.f = y.g在IR中会被转化为:

1
2
[21@L16] temp$8 = x.<X: int f>;
[22@L16] y.<Y: int g> = temp$8;

与之类似的, Invoke, BinaryExp也具有相同的特性.

如果不确定某条语句在框架中如何表示, 可以自己设计测试样例通过Assignment分析其结果.

回到这次实验, 可以简单认为所有AssignStmt的左值和右值中最多只有一个是Field/Array, 另外一个是Var.

InterSolver与InterConstPropagation

InterConstPropagation的字段可以简单的通过参数的方式进行传递, 但InterSolver与InterConstPropagation间该如何通信?

注意到InterConstantPropagation extends AbstractInterDataflowAnalysis, 其父类中含有字段InterSolver solver, 可以通过solver.xxx实现通信.

对于其中的private和protected字段, 可以为其编写一个public XType getX()API提供访问接口.(如result, worklist等).

数据结构Map

本次实验中存在大量"一对多"的联系, 可以考虑选取MultiMap进行维护. 其中提供了不少相当便捷的API.

relevantStmt

如果能把字段中的Var取出, 可以使用其中的APIvar.getStoreField()等API方便的获取有关语句, 不过对Static就没有太好的方法了, 笔者采用的是遍历icfg.getNodes().

FieldStmt, FieldAccesss, FiledRef & JField

Tai-e框架中的Field的处理要比Array复杂不少, 笔者在此做简要解释.

  • JField的结构是<Type: FieldName>, 可以使用FieldStmt.getRef().resolve()得到. 当使用Stmt解析出JField进行比较时会获取更高的精度. (笔者因为这个卡了hidden test)

  • 如果想获取Field的Obj(即base部分), 可以使用FieldStmt.getFieldAccess().getBase(). 不过需要先转换为InstanceFieldAccess类型才能使用getBase()的API.

    Tips: 笔者在此吐槽一句, 为何关于Field的API都封装在了tai-e-Assignemnt.jar中而不是显式的给出, 增大了如何处理Field的学习成本.

ArrayStmt

Array的结构相对简单一点, 通过getAccess()就可以简单的access.getBase/Index()获取需要的信息.

总结

恭喜挺过了本学期SPA的实验大魔王, 自己设计算法还是颇有难度的, 接下来迎接较为轻松的A8吧. (^_^)