LaPluma

Keep it simple and stupid.

0%

LeetCode个人题解[C++] P4 寻找两个正序数组的中位数

发表于 更新于 分类于 阅读次数：
本文字数： 3.3k 阅读时长 ≈ 6 分钟

题目链接: LeetCode|4.寻找两个正序数组的中位数

题面解释

找出两个有序数组合并后的中位数. 但要求时间复杂度\(\mathit{O}(log(m + n))\).

解法一 二分

笔者看到复杂度\(\mathit{O}(log(m + n))\)第一想法便是二分, 但怎么二分? 两个数组只是内部有序, 两个数组并不有序, 常规对数组二分的思路肯定是不行的.

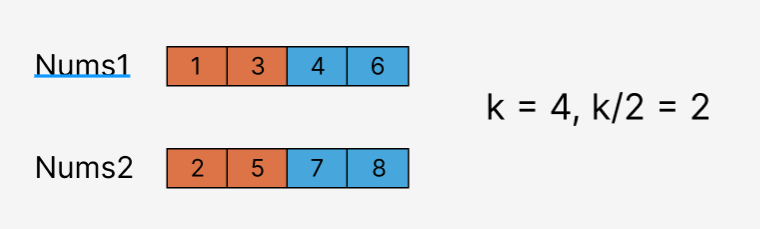
那该如何进行二分呢, 对答案进行二分. 令k为所寻找的k阶数, 初始为中位数, 则此时我们取两个数组的前\(k/2\)部分出来, 比较\(nums1[k/2]\)和\(nums2[k/2]\), 则可以直接排除\(k/2\)个数. 我们以下图例子来解释.

\(m = n = 4\), 我们有 \(k = 4, k/2 = 2\), 于是我们取两个数组的前两位, 比较3和5, 不难看出, 1和3不可能是中位数. 为什么? 因为1和3的阶必定小于\(k = 4\), 即便第一个数组的3比第二个数组的5前面所有数都大, 3的阶也只能是3, 1就更不必说了. 而5前面的数可能大于3后面的数(例子中未能体现, 读者可以自行构造一个满足这种情况的简单例子). 因此通过这种操作, 我们可以排掉 \(k/2\) 个不可能是中位数的元素, 接着我们令\(k = k - k/2\), 将被排除的数去掉, 重新进行上述过程.

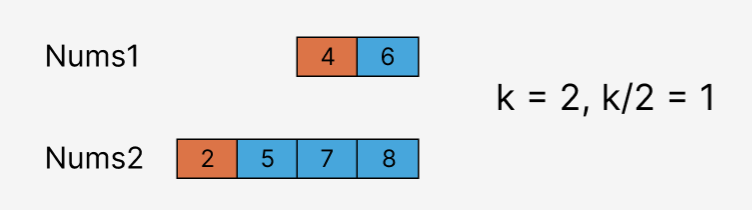
选取两个数组的前1位.比较2 和 4, 可以排除掉2. 此时过程进行到了边界处, 接下来\(k = 1\)无法继续了. 而此时剩下的4和5正是我们需要的中位数.

Tips: 为什么第二个数组不是选择2, 5, 7?

因为我们在上面的步骤中无法确定2和5是中位数与否, 此时的有效信息不足. 而把2 5 7都放进来与4进行比较会出现bug, 以上例, 4会被错误的排除掉

k为奇数时情况稍有不同, 但大多是一些细节问题, 笔者在此不再赘述. 推荐读者自己构建一个例子去推算上面的过程, 相信不难理解其中要义.

每次排除\(k/2\), 而 \(k = (m + n + 1) / 2\), 故时间复杂度\(\mathit{O}(log(m + n))\).

参考代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size();
        int n = nums2.size();
        //cout << m << " " << n << endl;
        //for(int i = 0; i < m; i++){cout << nums1[i] << " ";} cout << endl;
        //for(int j = 0; j < n; j++){cout << nums2[j] << " ";} cout << endl;

        int left1 = 0;
        int left2 = 0;

        int k = (m + n - 1) >> 1; // 排除掉小于中位数的数

        while (k > 1) {
            // 一个数组被清空
            if (left1 == m) {
                left2 += k;
                k = 0;
                break;
            }
            if (left2 == n) {
                left1 += k;
                k = 0;
                break;
            }
            
            int mid = k >> 1; // 注意循环条件 k > 1

            int mid1 = left1 + mid - 1;
            int mid2 = left2 + mid - 1;

            // 边界情况，剩余数组大小不足k
            if (left1 + mid > m) { // 等价于 left1 + mid - 1 >= m
                mid1 = m - 1;
            }
            if (left2 + mid > n) {
                mid2 = n - 1;
            }

            if (nums1[mid1] >= nums2[mid2]) {
                k -= mid2 - left2 + 1; // 一轮可以排除掉一半
                left2 = mid2 + 1;
            } else {
                k -= mid1 - left1 + 1;
                left1 = mid1 + 1;
            }
        }

        // 处理 k == 1
        if (k == 1) {
            if (left1 == m) {
                left2++;
            } else if (left2 == n) {
                left1++;
            } else {
                if (nums1[left1] >= nums2[left2]) {
                    left2++;
                } else {
                    left1++;
                }
            }
        }

        // 别忘了处理边界情况
        if ((m + n) & 1 == 1) { // 奇数
            if (left1 == m) {
                return nums2[left2];
            }
            if (left2 == n) {
                return nums1[left1];
            }
            return std::min(nums1[left1], nums2[left2]);
        } else { // 偶数
            if (left1 == m) {
                return (nums2[left2] + nums2[left2 + 1]) * 1.0 / 2;
            }
            if (left2 == n) {
                return (nums1[left1] + nums1[left1 + 1]) * 1.0 / 2;
            }

            int num1;
            if (nums1[left1] >= nums2[left2]) {
                num1 = nums2[left2];
                left2++;
            } else {
                num1 = nums1[left1];
                left1++;
            }
            int num2;
            if (left1 == m) {
                num2 = nums2[left2];
            }
            else if (left2 == n) {
                num2 = nums1[left1];
            }
            else{
                num2 = min(nums1[left1], nums2[left2]);
            }
            return (num1 + num2) * 1.0 / 2;
        }

        return 0;
    }
};

Tips: 本题思路并不难想出或者说并不难理解, 但非常考验代码功底, 对细节和边界情况的考察更像是此题的侧重点. 还望看到此处的读者能静下心来调试代码, 祝早日AC.

解法二 分割

笔者阅读题解时注意到的巧妙的解法, 原链接在此P4|windliang

更详细的数学证明, 思路和代码请阅读原文, 笔者在此只给出自己对其的理解.

本质来说, 两种方法殊途同归, 但分割的方法较为巧妙一些. 中位数, 或者说k阶数, 就是将数组分为两个部分, 其一是比k阶数小的部分, 其二是比k阶数大的部分.

对于有序的一个数组, 其性质本身就已经满足, 我们不妨将两部分简称为左半部分(小)和右半部分(大). 对于两个有序数组, 情况是一样的, 如果存在一种划分, 满足左边最大MaxLeft小于右边最小MinRight, 我们则认为这是关于k阶数的一种有效划分.

因此, 这道题就被转化为寻找数组中满足中位数的有效划分, 关于特定k阶数划分, 还需要满足左半部分和右半部分的数量关系, 若规定将k阶数划在左半部分, 则左半部分有k个元素, 右半部分有 n - k 个元素.

后面的事情就简单了, 固定数组1的划分位置, 根据数量关系找到数组2待判定划分位置, 根据MaxLeft和MinRight的大小关系决定数组1划分位置的左移或右移, 该过程可以通过二分完成.